Nous avons vu (article 17) qu’une structure dissipative est un système hors équilibre. Le déséquilibre peut être dû à une différence (gradient) de température, de pression, de potentiel, etc… Dans la suite de ce blog on parlera de façon générale de tension ou de stress. Plus la tension est grande, plus le déséquilibre est important.
L’expérience montre que lorsque le déséquilibre est suffisamment faible, le flux d’énergie est proportionnel à la tension. C’est le cas par exemple de la conduction, où le flux de chaleur est proportionnel à la différence de température. C’est le cas des écoulements laminaires où la vitesse du fluide est proportionnelle à la différence de pression. C’est aussi le cas du courant électrique qui est proportionnel à la différence de potentiel (loi d’Ohm). On est alors dans le domaine linéaire des relations d’Onsager.
Lorsque le déséquilibre d’un système augmente, sa structure peut devenir instable. Les instabilités qui apparaîssent provoquent un changement de structure. Le système se réorganise de lui-même. Une nouvelle structure apparaît, plus favorable au flux d’énergie. On appelle cela une bifurcation. C’est le mécanisme d’auto-organisation de l’univers (article 19).
Une bifurcation se produit lorsqu’il y a compétition entre plusieurs structures possibles. La structure adoptée est toujours celle qui favorise le plus le flux d’énergie. Parfois deux structures sont possibles, symétriques l’une de l’autre. Elles sont alors énergétiquement équivalentes. Le système choisit au hasard une des deux solutions. On dit qu’il y a rupture de symétrie. L’auto-organisation de l’univers en est parsemée d’exemples (article 19). Les ruptures de symétrie sont une caractéristique des bifurcations.
Une autre caractéristique des bifurcations est le phénomène d’hystérésis. Lorsque l’équilibre d’un système est modifié et que celui-ci franchit un point de bifurcation où une restructuration devient possible, celle-ci ne se produit pas immédiatement. Il y a retard à la réorganisation dans un sens comme dans l’autre. La transformation est en en partie irréversible. Cela entraîne une certaine stabilité des structures dissipatives et une mémorisation temporaire d’information sur lesquelles nous reviendrons.
En mathématiques, l’étude des bifurcations fait partie de l’analyse des systèmes dynamiques. Les mathématiciens ont mis en évidence de nombreux types de bifurcations et les ont classées suivant les caractéristiques des instabilités mises en jeu. Je me contenterai de décrire ici à titre d’exemple le modèle évolutif dit “logistique” de Pierre-François Verhulst. Les lecteurs non-mathématiciens pourront aisément sauter les équations.
A la suite des publications de Malthus, ce mathématicien belge a proposé de modéliser la croissance d’une population par une équation différentielle donnant l’accroissement dN du nombre N d’individus dans l’intervalle de temps dt. Sous sa forme moderne, cette équation s’écrit:
dN/dt = r.N.(1 – N/K)
où r est le taux de croissance de la population et (1 – N/K) est un facteur correctif imposé par des ressources limitées. On retrouve ici les notations r et K correspondant aux deux modes de sélection naturelle (r et K) mentionnés dans l’article 17. La solution de cette équation différentielle est une sigmoïde. Une population initialement faible s’accroît rapidement puis se stabilise à la valeur K.
Si l’on discrétise cette équation différentielle, on obtient la suite logistique liant la valeur de la population à l’instant t+1 à sa valeur à l’instant t. Dans cette expression, X = N/Nmax est le rapport (compris entre 0 et 1) de la population N à sa valeur maximale Nmax.
X(t+1) = μ.X(t).[1-X(t)].
Il est remarquable qu’une équation aussi simple donne lieu à tous les comportements typiques d’un système dynamique non-linéaire, comportements que nous allons brièvement décrire.
Si μ est inférieur à 1, la population va bien sûr s’éteindre. Si μ est compris entre 1 et 3, la population croît et se stabilise à la valeur
(μ-1)/μ. Pour les valeurs de μ très voisines de 1, cette valeur est proportionnelle au taux de croissance μ-1. C’est le domaine linéaire dont nous avons parlé plus haut. Au delà de μ = 3, l’évolution devient instable. C’est la première bifurcation. Pour 3 < μ < 3,449… la population oscille entre deux valeurs différentes correspondant aux deux branches de la figure ci-dessous. Au delà de μ = 3,449… la population oscille alternativement entre 4 valeurs, puis 8 valeurs, 32 valeurs, etc… (voir figure). Au delà de μ = 3,57…, le chaos s’installe. De très légères variations des conditions initiales conduisent à des résultats radicalement différents. L’évolution du système devient imprévisible sauf pour quelques valeurs de μ exceptionnelles pour lesquelles on observe à nouveau des oscillations périodiques. Un système dynamique non-linéaire est ainsi caractérisé par toute une famille de bifurcations conduisant à un chaos dynamique.
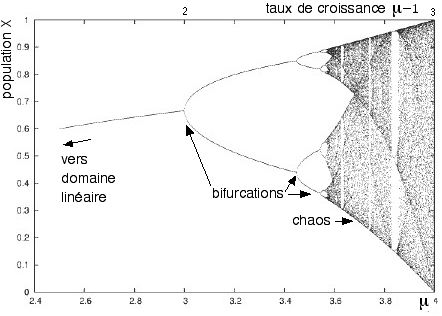
|
| Valeurs limites de la suite logistique |
Nous avons déjà vu deux exemples physiques de bifurcations pris en dynamique des fluides. L’un est le passage de la conduction à la convection (article 10). L’autre est le passage d’un écoulement laminaire à un écoulement turbulent (article 11). Dans ces exemples, un système initialement linéaire (flux proportionnel à la tension) devient non linéaire. Si l’on continue à accroître la tension de nouvelles bifurcations peuvent se produire menant peu à peu vers le chaos. On peut comparer le mouvement périodique du fluide dans une cellule de Bénard aux oscillations de la suite logistique. Dans ces exemples, il y a aussi rupture de symétrie. Dans une cellule convective ou un tourbillon le fluide peut tourner dans un sens ou dans un autre, souvent au hasard.
Il est intéressant de décrire l’apparition de telles instabilités à l’échelle microscopique. Je le ferai ici dans le cas du passage de la conduction à la convection (1). Ce passage se produit lorsque le gradient de température devient suffisamment important. Considérons une molécule du fluide dans l’expérience de Bénard (article 10). Cette molécule est agitée d’un mouvement brownien d’autant plus rapide que la température du fluide est plus élevée.
Supposons qu’à un moment donné, après un choc, la vitesse de cette molécule soit dirigée vers le haut. Entre deux chocs successifs, elle va parcourir une distance de l’ordre de son libre parcours moyen.
Si au bout de ce parcours la température du fluide n’a pas sensiblement changé, un nouveau choc va l’envoyer aussi bien vers le bas que vers le haut. En moyenne, elle va errer (on dit aussi diffuser) lentement. On dit qu’il y a équilibre thermodynamique local.
Si au contraire la température a sensiblement diminué alors, faute d’énergie suffisante, un nouveau choc a peu de chances de l’arrêter dans son mouvement ascendant. Plus elle monte, plus la température diminue et moins son mouvement a de chances d’être arrêté. Il y a instabilité. D’autres molécules de son entourage vont se trouver dans la même situation. Ces molécules vont former une zone de fluide chaud au milieu d’un fluide plus froid. Propulsé par la poussée d’Archimède un courant ascendant se forme. La convection apparaît. Nous retiendrons ici que, de façon générale, il y a instabilité, donc bifurcation, si l’environnement change de façon notable entre deux transferts d’énergie, c’est-à-dire lorsqu’il n’y a plus équilibre thermodynamique local.
Au point de bifurcation, on dit parfois que le système est dans un état critique. Dans notre prochain blog, nous verrons comment les états critiques s’auto-organisent.
(1) Ce phénomène est décrit par un système d’équations non-linéaires appelé système de Lorentz.
Liens internet:
http://fr.wikipedia.org/wiki/Théorie_d’Onsager
http://fr.wikipedia.org/wiki/Hystérésis
http://fr.wikipedia.org/wiki/Système_dynamique
http://fr.wikipedia.org/wiki/Modèle_évolutif_r/K
http://fr.wikipedia.org/wiki/Pierre_François_Verhulst
http://fr.wikipedia.org/wiki/Espèce_à_stratégie_r
http://fr.wikipedia.org/wiki/Espèce_à_stratégie_K
http://fr.wikipedia.org/wiki/Sigmoïde_(mathématiques)
http://fr.wikipedia.org/wiki/Fonction_logistique
http://fr.wikipedia.org/wiki/Théorie_du_chaos
http://fr.wikipedia.org/wiki/Mouvement_brownien
http://fr.wikipedia.org/wiki/Libre_parcours_moyen
http://fr.wikipedia.org/wiki/Équilibre_thermodynamique
Sur les propriétés des bifurcations voir aussi (classés par ordre de difficulté croissante):
• en français:
http://www.bibmath.net/dico/index.php3?action=affiche&quoi=./l/logistique.html
http://pilat.free.fr/tech/bif_gif.htm
• en anglais:
http://www.redfish.com/research/SchneiderKay1995_OrderFromDisorder.htm
http://berglund.univ-tln.fr/hystabt.html
http://www.saltspring.com/brochmann/math/chaos/chaos-3/chaos-3.00.html
http://mathworld.wolfram.com/LogisticMap.html
http://www.egwald.com/nonlineardynamics/
Lectures
James Gleick – La théorie du chaos: vers une nouvelle science (Flammarion, 1999)
M. Mitchell Waldrop – Complexity: the emerging science at the edhe of order and chaos (Simon & Schuster, 1992)
Edward N. Lorentz – The essence of chaos (U. of Washington Press, 1996)
Comment passe-ton de
dN/dt = r.N.(1 – N/K)
à
X(t+1) = μ.X(t).[1-X(t)]
?
Bonjour.
Il me semble me rappeler que Prigogine se sert de cette bçifurcation pour s’attaquer au déterminisme. Ce graphe montre que la bifurcation (le saut d’ une branche à l’ autre) ne dépend pas de la précision de la variable mu.
Même à 43 décimales, on ne peut prédire le choix.
Le chaos est dit déterminisme du fait que la prédiction et la localisation d’ un attracteur stabilisé peut être considéré comme déterministe (provisoire)