Dans ce blog j’ai proposé de définir une notion de température pour l’économie (billet 49), comme étant l’inverse T du coût de l’énergie. Plus l’énergie est bon marché, plus la température tend à être élevée et plus l’activité économique est importante. J’ai utilisé cette notion dans plusieurs publications notamment le chapitre 10 de l’ouvrage collectif d’Agnès Sinaï « Économie de l’après-croissance » (1).

Dans mon exposé au Shift-Project du mois de mars 2015 (vidéo du billet 75), j’ai défini de même une notion de potentiel P pour une production économique, comme étant le potentiel de Gibbs associé au volume V de la production (2). J’ai montré l’analogie entre les cycles de production d’une entreprise et les cycles de Carnot d’un gaz de volume V, de pression P et de température T. Nous allons poursuivre ici l’analogie entre les échanges économiques et ceux entre les molécules d’un gaz.

On sait que que pour un gaz dit «parfait», les variables P, V et T sont liées par la relation PV = RT, appelée équation d’état. R est la constante des gaz parfaits. L’analogue économique d’un gaz parfait serait une ensemble d’agents indépendants procédant à des échanges commerciaux au cours de rencontres fortuites. De même que les molécules d’un gaz parfait ne sont pas liées entre elles, de même les agents d’une telle économie agissent indépendamment les uns des autres.

Appliquée à la production économique, la relation des gaz parfaits implique un potentiel économique P d’autant plus grand que le volume V de la production est plus faible. C’est le cas des produits de luxe. Une robe d’un grand couturier a d’autant plus de valeur que peu de gens peuvent se l’offrir. Cette robe est d’autant plus économiquement intéressante, qu’elle ne coûte pas excessivement cher à fabriquer, c’est-à-dire que la température économique est suffisamment élevée (i.e. que l’économie est plus prospère). On n’achète pas des robes de grand couturier dans une économie de pénurie. De même que l’équation d’état des gaz parfaits s’applique aux températures élevées, de même elle s’applique aux économies d’abondance.

On sait que l’équation d’état des gaz réels diffère de celle des gaz parfaits d’autant plus qu’on se rapproche des températures auxquelles le gaz se condense et devient liquide. Dans ces conditons, les molécules suffisamment proches peuvent s’attirer, créant des liaisons temporaires. Diverses expressions analytiques ont été proposées pour tenir compte de ces liaisons. La plus utilisée est l’équation de van der Waals dont l’équation d’état s’écrit:

(P + a/V²)(V-b) = RT

Comparée à l’équation des gaz parfaits, l’équation de van der Waals contient deux termes correctifs. Le premier a/V² est le terme correctif sur la pression. Le second b est le terme correctif sur le volume.

Dans ce modèle, l’attraction entre les molécules crée une pression interne supplémentaire inversement proportionnelle au carré du volume. Quant au volume du gaz, il ne saurait être inférieur au volume b de ses molécules. L’importance de ce modèle est que, dans le plan (P,V), ses isothermes rendent bien compte de l’existence d’un point critique en dessous duquel le gaz peut devenir instable et se condenser en une phase liquide et une phase vapeur (3).

Appliquée à la production économique, l’équation de van der Waals implique l’existence d’un potentiel économique supplémentaire de la forme a/V². Pour un gaz réel il est spécifique à certaines molécules. Pour une production économique, il serait spécifique à certaines productions. Comme tout potentiel a/V² est une grandeur intensive, c’est-à-dire qu’elle ne dépend pas du volume de la production. Cela implique que le coefficient «a» croit comme le carré du volume V de la production. Il s’applique à des denrées dont le potentiel est d’autant plus grand qu’elles sont produites en grande quantité.

On peut donner comme exemple le téléphone portable. Celui-ci est d’autant plus utile que les autres en sont aussi équipés. Loin d’être un produit de luxe, il est devenu aujourd’hui une nécessité, par exemple pour ceux qui cherchent un domicile ou un emploi. De même, l’équation de van der Waals implique un volume de production minimal «b» que l’on pourrait qualifier de volume de survie.

Le cas général est intermédiaire entre l’économie d’abondance et l’économie de pénurie. Les économistes associent souvent à un même produit deux valeurs différentes, sa valeur d’échange et sa valeur d’usage. On peut considérer ces deux valeurs comme deux termes différents de leur potentiel économique. Un bon exemple est la propriété immobilière. Dans une économie d’abondance, la propriété immobilière est considérée comme un placement: sa valeur d’échange domine. Dans une économie de pénurie, c’est sa valeur d’usage qui est importante.

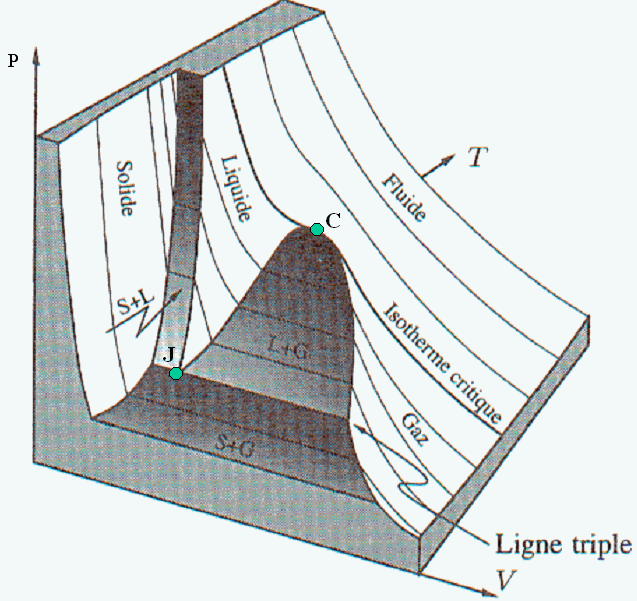
On peut représenter l’état d’un fluide quelconque par un point dans l’espace des trois variables P,V,T. Ces trois variables étant liées par une relation d’état, le point représentatif du fluide se trouve sur une surface, représentée sur la figure ci-dessous. Au voisinage du point critique C, cette surface peut être retrouvée à partir de l’équation de Van der Waals (3). Les zones sombres indiquent les régions de la surface pour lesquelles deux phases différentes subsistent en présence l’une de l’autre: solide et liquide (S+ L), solide et gaz (S + G), ou liquide et gaz (L + G). Projetée dans le plan (P,T), cette surface redonne la figure 1 de mon livre (4).

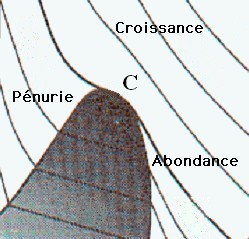
Si on applique ce résultat à une production économique, les trois variables sont alors le volume V de la production (quantités produites), le potentiel P de la production (exprimant la demande) et la température T de l’économie (exprimant d’offre). Au voisinage du point critique, le résultat est représenté sur la figure ci-dessous:

La zone pour laquelle le volume V de la production est faible, mais la demande P est élevée correspond à une économie de pénurie. Celle pour laquelle le volume V est élevé, mais la demande P est faible correspond à une économie d’abondance, voire de surproduction. Enfin, celle pour laquelle la température de l’écononomie est la plus haute (offre élevée) est une zone de forte croissance économique.

Comme pour la figure précédente, la zone sombre est une zone à l’intérieur de laquelle deux phases co-existent en présence l’une de l’autre. Ici une économie de pénurie subsiste en présence d’une économie d’abondance. On sait qu’au point critique C, la distribution des richesses suit une loi de puissance appelée loi de Pareto (5). Lorsqu’on pénètre dans la zone sombre, la classe moyenne s’effondre, laissant en présence deux économies distinctes, celle des gens riches et celle des gens pauvres. Comme le liquide se sépare de la vapeur, ces deux économies tendent à se séparer l’une de l’autre. Dans notre prochain billet, nous montrerons que c’est la région à l’intérieur de laquelle les sociétés s’effondrent.

(1) François Roddier. De la nécessité d’une décroissance. Dans: Agnès Sinaï, Économie de l’après-croissance, Politique de l’Anthropocène II, chapitre 10. Éditions SciencesPo (2015).

(2) François Roddier. La thermodynamique des transitions économiques. Dans: Res-Systemica, vol. 14, article 01 (septembre 2015).

(3) Voir Wikipedia: Équation d’état de van der Waals.

(4) François Roddier. Thermodynamique de l’évolution. Édit. Parole (2012), figure 1, p. 40.

(5) François Roddier. Thermodynamique de l’évolution. Édit. Parole (2012), section 13.5, p.123.