Dans ce blog j’ai proposé de définir une notion de température pour l’économie (billet 49), comme étant l’inverse T du coût de l’énergie. Plus l’énergie est bon marché, plus la température tend à être élevée et plus l’activité économique est importante. J’ai utilisé cette notion dans plusieurs publications notamment le chapitre 10 de l’ouvrage collectif d’Agnès Sinaï « Économie de l’après-croissance » (1).

Dans mon exposé au Shift-Project du mois de mars 2015 (vidéo du billet 75), j’ai défini de même une notion de potentiel P pour une production économique, comme étant le potentiel de Gibbs associé au volume V de la production (2). J’ai montré l’analogie entre les cycles de production d’une entreprise et les cycles de Carnot d’un gaz de volume V, de pression P et de température T. Nous allons poursuivre ici l’analogie entre les échanges économiques et ceux entre les molécules d’un gaz.

On sait que que pour un gaz dit «parfait», les variables P, V et T sont liées par la relation PV = RT, appelée équation d’état. R est la constante des gaz parfaits. L’analogue économique d’un gaz parfait serait une ensemble d’agents indépendants procédant à des échanges commerciaux au cours de rencontres fortuites. De même que les molécules d’un gaz parfait ne sont pas liées entre elles, de même les agents d’une telle économie agissent indépendamment les uns des autres.

Appliquée à la production économique, la relation des gaz parfaits implique un potentiel économique P d’autant plus grand que le volume V de la production est plus faible. C’est le cas des produits de luxe. Une robe d’un grand couturier a d’autant plus de valeur que peu de gens peuvent se l’offrir. Cette robe est d’autant plus économiquement intéressante, qu’elle ne coûte pas excessivement cher à fabriquer, c’est-à-dire que la température économique est suffisamment élevée (i.e. que l’économie est plus prospère). On n’achète pas des robes de grand couturier dans une économie de pénurie. De même que l’équation d’état des gaz parfaits s’applique aux températures élevées, de même elle s’applique aux économies d’abondance.

On sait que l’équation d’état des gaz réels diffère de celle des gaz parfaits d’autant plus qu’on se rapproche des températures auxquelles le gaz se condense et devient liquide. Dans ces conditons, les molécules suffisamment proches peuvent s’attirer, créant des liaisons temporaires. Diverses expressions analytiques ont été proposées pour tenir compte de ces liaisons. La plus utilisée est l’équation de van der Waals dont l’équation d’état s’écrit:

(P + a/V²)(V-b) = RT

Comparée à l’équation des gaz parfaits, l’équation de van der Waals contient deux termes correctifs. Le premier a/V² est le terme correctif sur la pression. Le second b est le terme correctif sur le volume.

Dans ce modèle, l’attraction entre les molécules crée une pression interne supplémentaire inversement proportionnelle au carré du volume. Quant au volume du gaz, il ne saurait être inférieur au volume b de ses molécules. L’importance de ce modèle est que, dans le plan (P,V), ses isothermes rendent bien compte de l’existence d’un point critique en dessous duquel le gaz peut devenir instable et se condenser en une phase liquide et une phase vapeur (3).

Appliquée à la production économique, l’équation de van der Waals implique l’existence d’un potentiel économique supplémentaire de la forme a/V². Pour un gaz réel il est spécifique à certaines molécules. Pour une production économique, il serait spécifique à certaines productions. Comme tout potentiel a/V² est une grandeur intensive, c’est-à-dire qu’elle ne dépend pas du volume de la production. Cela implique que le coefficient «a» croit comme le carré du volume V de la production. Il s’applique à des denrées dont le potentiel est d’autant plus grand qu’elles sont produites en grande quantité.

On peut donner comme exemple le téléphone portable. Celui-ci est d’autant plus utile que les autres en sont aussi équipés. Loin d’être un produit de luxe, il est devenu aujourd’hui une nécessité, par exemple pour ceux qui cherchent un domicile ou un emploi. De même, l’équation de van der Waals implique un volume de production minimal «b» que l’on pourrait qualifier de volume de survie.

Le cas général est intermédiaire entre l’économie d’abondance et l’économie de pénurie. Les économistes associent souvent à un même produit deux valeurs différentes, sa valeur d’échange et sa valeur d’usage. On peut considérer ces deux valeurs comme deux termes différents de leur potentiel économique. Un bon exemple est la propriété immobilière. Dans une économie d’abondance, la propriété immobilière est considérée comme un placement: sa valeur d’échange domine. Dans une économie de pénurie, c’est sa valeur d’usage qui est importante.

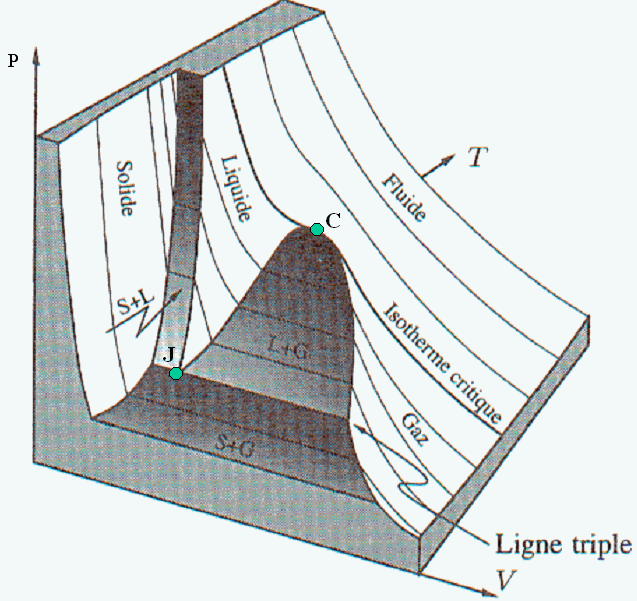
On peut représenter l’état d’un fluide quelconque par un point dans l’espace des trois variables P,V,T. Ces trois variables étant liées par une relation d’état, le point représentatif du fluide se trouve sur une surface, représentée sur la figure ci-dessous. Au voisinage du point critique C, cette surface peut être retrouvée à partir de l’équation de Van der Waals (3). Les zones sombres indiquent les régions de la surface pour lesquelles deux phases différentes subsistent en présence l’une de l’autre: solide et liquide (S+ L), solide et gaz (S + G), ou liquide et gaz (L + G). Projetée dans le plan (P,T), cette surface redonne la figure 1 de mon livre (4).

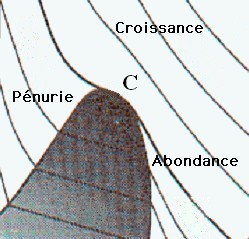
Si on applique ce résultat à une production économique, les trois variables sont alors le volume V de la production (quantités produites), le potentiel P de la production (exprimant la demande) et la température T de l’économie (exprimant d’offre). Au voisinage du point critique, le résultat est représenté sur la figure ci-dessous:

La zone pour laquelle le volume V de la production est faible, mais la demande P est élevée correspond à une économie de pénurie. Celle pour laquelle le volume V est élevé, mais la demande P est faible correspond à une économie d’abondance, voire de surproduction. Enfin, celle pour laquelle la température de l’écononomie est la plus haute (offre élevée) est une zone de forte croissance économique.

Comme pour la figure précédente, la zone sombre est une zone à l’intérieur de laquelle deux phases co-existent en présence l’une de l’autre. Ici une économie de pénurie subsiste en présence d’une économie d’abondance. On sait qu’au point critique C, la distribution des richesses suit une loi de puissance appelée loi de Pareto (5). Lorsqu’on pénètre dans la zone sombre, la classe moyenne s’effondre, laissant en présence deux économies distinctes, celle des gens riches et celle des gens pauvres. Comme le liquide se sépare de la vapeur, ces deux économies tendent à se séparer l’une de l’autre. Dans notre prochain billet, nous montrerons que c’est la région à l’intérieur de laquelle les sociétés s’effondrent.

(1) François Roddier. De la nécessité d’une décroissance. Dans: Agnès Sinaï, Économie de l’après-croissance, Politique de l’Anthropocène II, chapitre 10. Éditions SciencesPo (2015).

(2) François Roddier. La thermodynamique des transitions économiques. Dans: Res-Systemica, vol. 14, article 01 (septembre 2015).

(3) Voir Wikipedia: Équation d’état de van der Waals.

(4) François Roddier. Thermodynamique de l’évolution. Édit. Parole (2012), figure 1, p. 40.

(5) François Roddier. Thermodynamique de l’évolution. Édit. Parole (2012), section 13.5, p.123.

Un lecteur aura peut-être remarqué l’analogie entre la suite des α(i) du billet précédent et la suite logistique décrite dans mon billet 20:

Xi+1 = μ.Xi.[1-Xi]        (1)

Avec la même notation, la suite du billet précédent s’écrit:

Xi+1 = -μ.Xi.log Xi     (2)

Les deux fonctions X(1-X) et -X.log(X) ont un aspect tout à fait similaire pour X compris entre 0 et 1. La première est symétrique. Elle représente un arc de parabole avec un maximum égal à 1/4 pour X=1/2. La seconde est légèrement dissymétrique et passe par un maximum égal à 1/e pour X=1/e. On peut donc s’attendre à ce que les suites (1) et (2) aient un comportement analogue. À ma connaissance, personne ne l’a encore vérifié. Aussi ai-je profité d’un séjour à la neige avec mon fils ainé [1] pour lui demander de le vérifier. Mes lecteurs auront la primeur du résultat.

Les deux figures ci-dessous montrent la limite X de la suite en fonction du paramètre μ, la première dans le cas de la fonction logistique de Verhulst, la seconde dans le cas de la fonction d’Ulanowicz. On constate que l’allure générale est la même, avec toutefois une différence notable. Au lieu de démarrer à μ = 1, la courbe de la figure 2 démarre à μ = 0. Que cela signifie-t-il physiquement?

Les deux courbes correspondent à des modèles physiques notablement différents. Le modèle de Verhultz s’applique à une structure dissipative (originellement une société) dont l’organisation ne change pas, mais dont les ressources énergétiques diminuent. Le modèle d’Ulanowicz s’applique à une structure dissipative (originellement un écosystème) dont l’organisation évolue sans cesse et s’adapte à son environnement.

Il s’agit de deux conceptions radicalement différentes. La population de Verhultz ne se développe qu’en présence de ressources appropriées. Celle d’Ulanowicz s’adapte aux ressources disponibles. Le fait même de pouvoir s’adapter implique un rendement infini à l’origine (voir billet précédent). La population de Verhultz s’éteint lorsque ses ressources sont épuisées. La population d’Ulanowicz s’effondre dans la mesure ou elle ne s’adapte pas assez vite à d’autres ressources.

Le modèle d’Ulanowicz est clairement plus proche de la réalité. La fin du pétrole n’implique pas la fin de l’humanité. Elle implique un effondrement de nos sociétés actuelles dans la mesure où celles-ci ne développent pas assez vite de nouvelles ressources. On retrouve une fois de plus l’importance de la notion d’entropie par rapport à celle d’énergie. Une société ne s’effondre pas parce qu’elle épuise ses ressources en énergie mais parce qu’elle n’acquiert pas assez vite l’information nécessaire pour renouveler ses ressources, c’est-à-dire elle n’élimine pas assez vite l’entropie qu’elle produit [2][3].

[1] Nicolas Roddier (Tachysséma)

[2] François Roddier, dans Politiques de l’Anthropocène II. Économie de l’après-croissance, (Éd. SciencesPo). Chapitre 10: Pourquoi les économies stagnent et les civilisations s’effondrent.

[3] Jacopo Simonetta. The other side of the global crisis: entropy and the collapse of civilisations.

Fig. 1. Suite de Verhultz

Fig. 2. Suite d’Ulanowicz

Les économistes souhaiteraient faire de l’économie une science exacte au même titre que les sciences physiques. Ils tentent pour cela d’établir des relations mathématiques entre des grandeurs mesurables. Malheureusement, le choix de ces grandeurs est très pauvre. Il semble se limiter à deux. L’une est le temps qui est clairement défini. L’autre est la monnaie dont l’unité, autrefois liée à l’étalon or, est aujourd’hui plutôt mal définie, et semble fluctuer de façon incontrôlable.

Nous avons vu qu’une société humaine est une structure dissipative. Elle est modélisable comme un réseau d’agents échangeant de l’information. D’un point de vue strictement économique, l’information échangée est la monnaie. Il semble qu’on ait là de quoi jeter les bases d’une véritable science économique. Peut-on appliquer les résultats d’Ulanowicz à l’économie?.

On se heurte d’emblée à un problème fondamental lié à la notion de structure dissipative. Par définition, celles-ci sont dans un état stationnaire, c’est-à-dire qu’elles n’évoluent pas. Malheureusement on s’intéresse justement à leur évolution. Comment faire? En dynamique des fluides, on suppose que l’évolution d’un cyclone est suffisamment lente pour qu’on puisse encore définir la température et la pression du gaz en chaque point. C’est ce qu’on appelle l’équilibre thermodynamique local. Lorsqu’on mesure l’état d’un écosystème, on suppose implicitement que cet état ne varie pas sensiblement durant le temps des mesures. L’hypothèse apparait valable compte tenu de la précision des mesures. Qu’en est-il de l’économie?

Les économistes résolvent généralement le problème en définissant l’état d’une économie sur l’échelle d’une année. Ce choix naturel permet de moyenner les fluctuations saisonnières (mais peut poser des problèmes dans le cas très fluctuant de l’économie financière). Quelle serait donc l’équivalent du paramètre d’ordre α d’Ulanowicz? Si l’on définit l’information comme étant donnée par la monnaie, alors l’information mémorisée est le capital. Cette information est en général mémorisée sur un compte bancaire. Normalisée au maximum égal à 1, c’est la fraction α du revenu annuel qui est capitalisée en vue de rapporter l’année suivante.

La quantité α est une variable aléatoire dont la réalisation n’est connue qu’à la fin de l’année i. L’expression d’Ulanowicz montre que α(i) peut aussi être considéré comme un estimateur bayésien (1) de la probabilité de profit pour l’année i+1. En ce sens, α(i) apporte  pour l’année suivante une information α(i+1) qui vaut en moyenne α(i+1) = -α(i).log α(i). La quantité α(i+1) est ce qu’on appelle le revenu du capital. Les économistes la mettent sous la forme α(i+1) = r.α(i) où r est le rendement du capital. On voit que l’expression d’Ulanowicz implique un rendement du capital de la forme r = -log α. Cela peut paraître surprenant car il est infini à l’origine. Nous allons voir que c’est effectivement le cas.

Si l’on réinvestit chaque année le revenu du capital, on a ce qu’on appelle un revenu d’intétêts composés caractéristique des processus autocatalytiques. Une fois réinvesti le revenu du capital devient un nouveau capital α(i+1) = r.α(i), terme d’une progression géométrique de raison r. Il s’agit bien d’une cascade d’événements typique des processus d’auto-organisation. On sait que ces cascades sont déclenchées par des fluctuations aléatoires, ici des pertes ou des gains accidentels en moyenne nuls. Un gain de moyenne nulle peut être considéré comme un revenu accidentel sans capital. Son rendement est bien infini. Lorsque ce gain est investi, il peut engendrer une cascade plus ou moins importante d’événements capables de créer des fortunes. C’est la base du système capitaliste, souvent qualifié de « rêve américain », dans lequel n’importe qui est sensé pouvoir devenir riche.

L’expression d’Ulanowicz implique qu’il existe une valeur critique α  = 1/e (37%) pour laquelle la raison r = -log α de la progression est égale à l’unité. Le revenu du capital compense alors tout juste les dépenses et maintient le capital constant. Lorsque α < 1/e, la raison r de la progression est supérieure à l’unité, de sorte que le capital croit chaque année. Dans le cas d’un pays, on parle de croissance économique. Lorsque α > 1/e, la raison r de la progression devient inférieure à l’unité et le capital décroit. Lorsqu’il y a eu création monétaire, c’est-à-dire que le capital a été emprunté à une banque, alors il ne peut plus être remboursé et c’est la faillite, d’où la terreur des économistes à l’idée d’une décroissance économique.

Tout système économique, nation ou entreprise, cherche à maximiser le revenu de son capital de façon à faire croître ce dernier. On voit qu’il y a une limite au delà de laquelle le capital ne croit plus et même décroit, c’est le point critique caractérisé par le nombre sans dimension 1/e. Il semblerait que l’on puisse généraliser ce résultat à toute structure dissipative (2). Celle-ci va s’adapter à son environnement de façon à maximiser l’information reçue jusqu’au moment ou l’information qu’elle mémorise ne croit plus et même décroit. Elle a alors atteint le point critique. Elle mémorise alors autant d’information qu’elle en efface. Cela implique que le point critique est aussi un point de dissipation maximale d’énergie. On sait qu’une structure dissipative oscille constamment autour du point critique en quête du maximum (billet 21).

(1) Un estimateur bayésien (ou inférence bayésienne) estime la probabilité d’un événement à partir de celles d’événements précédents.

(2) Considérée comme un réseau d’agents échangeant de l’information.

Les frottements solides, la viscosité des liquides et des gaz font que l’énergie mécanique se dissipe toujours en chaleur. En l’absence d’apport extérieur d’énergie, les mouvements mécaniques finissent par s’arrêter, tandis que les différences de températures s’estompent et s’annulent. C’est ainsi que les systèmes isolés tendent vers l’équilibre thermodynamique. Leur énergie interne reste constante, tandis que leur entropie augmente pour atteindre sa valeur maximale à l’équilibre.

Supposons maintenant qu’on maintienne les mouvements mécaniques en compensant l’effet des frottements par à un apport permanent d’énergie, et que la chaleur dégagée soit évacuée de façon à ce que la température du système reste constante. On a maintenant un système ouvert maintenu en mouvement permanent grâce au flux d’énergie qui le traverse. Restant constamment semblable à lui-même, le système thermodynamique est qualifié de stationnaire.

Les exemples de tels systèmes abondent dans la nature: un cyclone ou un ensemble de cyclones/anticyclones tels que l’atmosphère terrestre, un être vivant ou un ensemble d’êtres vivants comme une espèce animale ou végétale, ou un écosystème, un être humain ou un ensemble d’êtres humains tel qu’une société humaine. Il y a environ un demi-siècle Prigogine leur donnait le nom de structure dissipative.

Par définition, une structure dissipative dissipe de l’énergie donc produit de l’entropie qu’elle évacue au fur et à mesure qu’elle la produit. Entropie et information étant de signe opposé (billet précédent), évacuer de l’entropie signifie importer de l’information. Une structure dissipative importe sans cesse de l’information de son environnement. Lorsqu’elle s’auto-organise une structure dissipative diminue son entropie interne, donc augmente son contenu en information en la mémorisant. C’est une mémoire temporaire.

En régime stationnaire, une structure dissipative perd autant d’information qu’elle en mémorise. Elle renouvelle sans cesse l’information qu’elle mémorise. Perdre de l’information est synonyme de produire de l’entropie, donc de dissiper de l’énergie. C’est en effaçant continuellement de l’information qu’elle a mémorisée qu’une structure dissipative dissipe de l’énergie.

S’il est naturel de parler de diminution d’entropie lorsqu’une machine thermique comme un cyclone s’auto-organise, parler d’information mémorisée est plus inhabituel. La mémoire d’un cyclone est inertielle. Si vous coupez la source d’énergie, le cyclone va continuer à tourner mais de moins en vite. La mémoire de ce mouvement va s’effacer progressivement au fur et à mesure que l’énergie se dissipe.

On sait aujourd’hui que les organismes vivants mémorisent de l’information dans leurs gènes. Les organismes les plus évolués ont aussi un cerveau. Un jeune enfant mémorise énormément d’information au cours de son éducation. Devenu adulte, il oublie autant de faits qu’il en mémorise de nouveaux. Devenu vieux, sa mémoire décline peu à peu, comme sa faculté de dissiper l’énergie. Les sociétés humaines ont longtemps mémorisé de l’information dans des livres. Aujourd’hui, leur faculté de mémoriser de l’information a considérablement augmenté, comme celle de dissiper de l’énergie.

J’ai déjà parlé dans ce blog du modèle de cerveau de Stassinopoulos et Bak (billet 62). Il est décrit dans mon livre sur la thermodynamique de l’évolution (sections 9.3 et 9.4). Ce modèle s’applique à un réseau neuronal quelconque. Il peut, par exemple, être utilisé pour comprendre le comportement d’une société humaine (billet 63). On parle alors de « cerveau global ». Il peut aussi être utilisé pour décrire un réseau d’échanges économiques (voir mon exposé au CNAM). Il pourrait même s’appliquer à un gaz, considéré comme un ensemble de particules qui échangent de l’information (billet 26).

Un cas particulierement intéressant est celui d’un écosystème. Après avoir reçu une formation d’ingénieur chimiste, Robert Ulanowicz s’est intéressé aux écosystèmes comme étant des réseaux d’agents échangeant de la matière, de l’énergie et de l’information. Il a ainsi modélisé les échanges entre les organismes vivants de la baie de Chesapeake. Pour Ulanowicz, les écosystèmes mémorisent de l’information tout comme le fait un cerveau humain. Il définit le degré d’ordre d’un écosystème par un paramètre α compris entre 0 et 1.

On peut interpréter ce paramètre d’ordre α comme étant la fraction de mémoire utilisée par ce réseau neuronal. Ses résultats s’appliquent à toute structure dissipative considérée comme un réseau neuronal. Nous avons vu plus haut qu’une structure dissipative s’auto-organise en mémorisant de l’information sur son environnement. Plus la quantité d’information mémorisée est grande, mieux la structure s’adapte à son environnement, mais plus elle doit modifier d’information pour rester adaptée, donc plus elle dissipe d’énergie. Il arrive un moment ou la fraction 1-α de mémoire disponible devient insuffisante, de sorte que les capacités d’adaptation de la structure n’augmentent plus et même diminuent. Il existe une valeur de α pour laquelle la capacité d’adaptation est optimale.

Robert Ulanowicz définit la robustesse R d’un écosystème comme étant sa capacité à s’adapter aux changements. Il montre que R doit être de la forme R = -α.log(α). La robustesse est nulle pour α = 0 et pour α = 1. Elle est maximale et égale à 1 pour α = 1/e où e est la base des logarithmes népériens (e = 2,718). Ses mesures sur les écosystèmes de la baie de Chesapeake montrent que les valeurs observées de α se concentrent effectivement autour de la valeur 1/e. Pour plus de détails voir l’article original (1). Dans un prochain billet, nous en tirerons les conséquences.

(1) R.E. Ulanowicz, Int. J. of Design & Nature and Ecodynamics. Vol. 4, No. 2 (2009) 83–96.

Beaucoup de mes lecteurs trouvent ces notions difficiles, notamment ceux d’entre eux qui n’ont pas eu de formation scientifique. Je les rassure. Les physiciens eux-mêmes ont mis plus d’un siècle à comprendre ce qu’est l’entropie.

Le concept d’entropie a été introduit en 1865 par le physicien allemand Rudolph Clausius, comme une conséquence du second principe de la thermodynamique, tel qu’il a été énoncé en 1824 par le français Sadi Carnot. Comme l’énergie, l’entropie est une fonction d’état, c’est-à-dire qu’elle ne dépend que de l’état (1) du système considéré. Cependant, à la différence de l’énergie, l’entropie n’est pas une quantité conservative. Elle ne se conserve que dans les systèmes isolés subissant des transformations réversibles. Si un système isolé subit des transformations irréversibles, son entropie augmente. Ainsi, l’entropie d’un système isolé ne peut qu’augmenter. Sa valeur maximale est atteinte à l’équilibre thermodynamique.

Cela a conduit à l’idée que l’entropie de l’univers ne peut qu’augmenter, idée que l’on retrouve partout dans la littérature. En pratique, la seule chose qu’un scientifique puisse étudier est l’univers observable. On sait aujourd’hui que l’univers observable perd sans cesse de la matière. Une partie de celle-ci disparait derrière un horizon cosmologique (2) tandis qu’une autre partie disparait à l’intérieur de trous noirs. En conséquence, l’entropie de l’univers observable peut fort bien diminuer. L’apparition spontanée de différences de température, lors de la formation des étoiles, laisse à penser que c’est le cas.

Dès 1861, Willard Gibbs soulevait une difficulté liée à la notion d’entropie en montrant que mélanger deux gaz augmente leur entropie, sauf si ceux-ci sont identiques. L’augmentation est la même aussi petite que ce soit leur différence. Ainsi l’entropie d’un système dépend de ce qu’on sait sur le système.

En 1868, James Clerk Maxwell aboutissait à une conclusion similaire en montrant qu’un « démon » qui serait capable de distinguer les molécules rapides d’un gaz de ses molécules lentes pourrait les séparer, sans effectuer de travail mécanique. Cela créerait une différence de température, en violation du second principe.

En 1929, Leo Szilard reprend l’idée de Maxwell et montre qu’on pourrait faire marcher un moteur thermique avec une seule source de chaleur en utilisant un gaz formé d’une seule molécule à la condition de savoir où celle-ci se trouve. Ces deux derniers exemples montrent qu’un apport de connaissance sur un système isolé diminue l’entropie de celui-ci.

En 1944, Erwin Schrödinger, remarque qu’en s’auto-organisant les êtres vivants diminuent leur entropie interne grâce au flux d’énergie qui les traverse. Il introduit le néologisme de néguentropie ou entropie négative.

En 1948, Claude Shannon publie sa théorie mathématique de la communication dans laquelle il introduit une mesure de la quantité d’information a transmettre dans un message. L’expression de cette mesure est identique (au signe près) à celle de l’entropie de Gibbs. On parle alors d’entropie informationelle ou entropie de Shannon.

En 1956, Léon Brillouin applique l’expression de Shannon à l’information apportée par le démon de Maxwell et montre qu’elle résoud le paradoxe. L’entropie thermodynamique de Gibbs apparait alors comme un cas particulier de l’entropie de Shannon appliquée à l’information sur un système thermodynamique. Appliquée aux êtres vivants, la néguentropie de Schrödinger représente l’information transmise par les gènes.

En 1961, les ingénieurs cherchent à réduire la chaleur dégagée par les ordinateurs et se posent la question de savoir s’il y a une limite théorique. Ralph Landauer montre qu’il y a une limite due aux opérations irréversibles. Effacer un bit d’information doit nécessairement provoquer un dégagement de chaleur équivalent à l’énergie d’un degré de liberté du système. C’est le principe de Landauer. Effacer de l’information étant un cas particulier d’opération irréversible, l’entropie de Shannon devient un cas particulier d’entropie thermodynamique.

Entropie thermodynamique et entropie de Shannon étant chacune un cas particulier de l’autre, cela implique qu’il s’agit d’un seul et même concept.

Aujourd’hui, les lasers permettent d’isoler un très petit nombre de particules élémentaires, d’observer leur agitation thermique et même de les manipuler comme le ferait un démon de Maxwell (3). C’est ainsi que le principe de Landauer a pu être récemment vérifié expérimentallement au laboratoire de l’ENS de Lyon (4).

Les travaux de Landauer ont montré que la notion d’information est bien une grandeur physique. Elle s’applique aussi bien à l’état d’un gaz qu’à celui d’un ordinateur. De fait, le physicien Ed Fredkin a montré qu’un gaz se comporte comme un ordinateur. L’univers lui-même peut être considéré comme un ordinateur (billet 26), un ordinateur qui se perfectionnerait de lui-même en créant des modules capables de mémoriser toujours plus d’information. Prolongements exosomatiques des cerveaux humains, les ordinateurs apparaissent eux-mêmes comme les derniers avatars de cette évolution.

(1) L’état thermodynamique d’un système est défini par ses variables macroscopiques. Par exemple, l’état d’un gaz est défini par son volume, sa pression et sa température.

(2) Lawrence M. Krauss, Robert J. Sherrer. The End of Cosmology? Scientific American, March 2008, pp. 47-53.

(3) Eric Lutz, Sergio Ciliberto, Information: From Maxwell’s demon to Landauer’s eraser. Physics Today, Vol. 68, Issue 9, September 2015.

(4) Antoine Bérut et al., 2012.

Le Contre-Sommet de Vénissieux a été annulé (voir le site). Je partage  l’émotion de tous devant des événements qui, hélas, confirment nos inquiétudes  sur l’évolution actuelle de la société. Voici le texte que j’avais préparé pour mon intervention:

Je souhaiterais ici vous faire part de mon expérience en tant que chercheur en sciences de l’univers (Astronomie-Géophysique). J’ai choisi cette voie en 1959 parce que j’étais plus intéressé par la recherche fondamentale que par ses applications. Je croyais alors naïvement que les chercheurs décidaient eux-mêmes des orientations les plus susceptibles de faire avancer nos connaissances. Je me suis rapidement aperçu que ces décisions étaient prises d’en haut par des technocrates, suivant des critères obscurs, généralement liés à d’éventuelles applications industrielles ou militaires.

Dans le cas de l’astronomie, cela me paraissait franchement bizarre jusqu’au jour où je me suis rendu compte que le critère principal était la faveur du grand public (il faut bien que nos dirigeants se fassent élire!). J’ai passé ensuite ma vie à tenter de détourner des moyens de financement de grands programmes aussi dispendieux qu’inutiles, vers des recherches qui me paraissaient à la fois moins coûteuses et bien plus prometteuses. Je disais alors à qui voulait l’entendre: on est en train de tuer la poule aux œufs d’or.

Aujourd’hui la poule est à l’agonie. Les partisans de la croissance s’en lamentent. Je crains que certains partisans de la décroissance ne s’en réjouissent. Je donne tort aux uns comme aux autres. La poule, c’est en fait toute notre civilisation. On sait aujourd’hui que les civilisations naissent, se développent, vieillissent et meurent. Lorsque j’étais jeune, je m’étonnais que les habitants de l’île de Pâques aient pu abattre tous leurs arbres sans se rendre compte de ce qu’ils faisaient. Je pensais qu’en aucun cas, une civilisation comme la nôtre ne ferait une telle bétise. C’est pourtant ce que nous avons fait en brûlant nos ressources fossiles au point de provoquer un réchauffement climatique. Aujourd’hui, les technocrates appellent au secours les chercheurs en sciences de l’univers. Ma réponse est: c’est trop tard!

Une aventure similaire est arrivée aux Mayas d’Amérique comme aux Sumériens de Mésopotamie. On parle aujourd’hui de «cerveau global». L’effondrement des civilisations conduit à une prise de conscience collective des individus qui la composent. Ceux-ci s’interrogent sur les causes de l’effondrement. Qu’avons nous fait? La civilisation méditerranéenne s’est effondrée en 1177 avant J.C., à la fin de l’âge de bronze. Vers cette époque apparaissait le monothéisme avec l’ancien testament. Celui-ci nous en offre une explication, celle du veau d’or: le dieu de Moïse nous puni à cause de notre cupidité. Mille six cents ans plus tard, l’empire romain s’effondre. Le nouveau testament nous propose une nouvelle explication: nous sommes punis à cause de nos disputes entre monothéistes et polythéistes. Le message est celui des chrétiens: aimons nous les uns les autres.

Ce message a présidé à l’essor du Moyen-Âge jusqu’à ce que de nouvelles querelles religieuses apparaissent. Celles-ci ont été surmontées au siècle des lumières. Celui-ci nous a conduit à la révolution industrielle, mais aussi au réchauffement climatique. Mille six cents ans après l’effondremement de l’empire romain, nous sommes à nouveau au bord du gouffre. Comment le cerveau global de l’humanité va-t-il réagir? Quel nouveau péché avons-nous commis? S’il parait difficile d’éviter de nouvelles querelles, la leçon semble claire: nous avons péché par orgueil. En mettant le pied sur la lune, l’homme a cru s’affranchir des lois de la nature. Comme le dit l’entrepreneur lyonnais Romain Ferrari, il est grand temps qu’il remette les pieds sur terre.

Si notre poule aux œufs d’or va s’éteindre, un de ses œufs va un jour éclore. Quel consigne allons-nous laisser à nos descendants? Pour moi, la réponse est claire: c’est une leçon d’humilité. Nous avons pour la première fois une explication rationnelle à ce qui nous arrive, mais elle est encore très mal comprise. La vie est un processus naturel de dissipation d’énergie. Nous sommes faits pour dissiper l’énergie. Dès qu’une source d’énergie apparait, nous nous précipitons vers elle comme les insectes vers la lumière à laquelle ils se brûlent. Allons-nous enfin en devenir conscient?

Une seule loi pourrait aujourd’hui remplacer les dix commandements de Moïse: la loi fondamentale de la thermodynamique, dite loi de Carnot. Elle s’énonce ainsi: on ne peut durablement dissiper l’énergie que par des cycles fermés de transformation extrayant de la chaleur d’une source chaude pour en rendre une partie à une source froide. Nous commençons seulement à en percevoir les implications. La première est que cette loi met en jeu non seulement l’Homme mais toutes les formes terrestres de dissipation d’énergie, un ensemble que certains dénomment Gaïa.

Une seule forme d’énergie est autorisée. Elle est fournie par le Soleil, notre source chaude à 6000°K. Notre source froide est le ciel nocturne à 3°K. Elle implique que nous prenions soin de la couche d’ozone qui nous en sépare. Quand au cycles de transformations, ils mettent en jeu toutes les formes de vie terrestre. On peut considérer Gaïa comme un moteur à deux temps. Dans un premier temps, les plantes captent l’énergie solaire et l’emmagazinent sous forme de carbone chimiquement réduit. Dans un second temps, l’oxydation du carbone dégage la chaleur émise sous forme de rayonnement infrarouge en direction du ciel nocturne.

Les moteurs thermiques sont naturellement instables. Ils fonctionnent grâce à des suites d’explosions et d’extinctions. James Watt a dû équiper sa machine à vapeur d’un régulateur à boule. L’humanité va devoir réguler son propre développement. Elle pourra pour cela s’inspirer de la biologie (on parle de biomimétisme). Elle devra passer d’un stade d’organisation semblable à celui des écosystèmes à l’intérieur duquel règne une compétition darwinienne, à un stade d’organisation plus complexe, semblable à celui d’un organisme multicellulaire. Cela implique le développement de multiples voies métaboliques, chacune associée à des monnaies-enzymes différentes. Elles sont la clé des mécanismes de régulation du corps humain.

Ceux qui le désirent pourront me rencontrer au « Contre-sommet mondial sur le climat » à Vénissieux le samedi 14 novembre 2015.

Mercredi 14 octobre 2015 à 19h30, je donnerai une des deux conférences animées par Philippe Lamberts, à:

La Tricoterie, 158 rue Théodore Verhaegen, 1060 St-Gilles, Belgique.

Il est recommandé de s’inscrire à l’avance par e mail via: info@etopia.be ou la page facebook.

Une société d’insectes, comme un essaim d’abeilles, ne peut se former que si les individus qui la composent ont tous des gènes communs, en l’occurrence les gènes de la reine qui est leur génitrice commune. Ce sont ces gènes communs qui assurent la cohésion de la société grâce au phénomène de sélection de parentèle. Par contre les mâles appelés faux bourdons communiquent à leurs descendants des gènes différents. En assurant la diversité génétique de l’essaim, ils permettent à la sélection naturelle d’agir sur son évolution.

On sait que, chez l’Homme, la culture joue le rôle des gènes (1). De la même façon, la cohésion d’une société humaine nécessite une certaine proportion de culture commune à tous ses membres. Cette culture commune ne peut être dispensée que par une éducation commune. Elle donne le sens d’appartenance à une même communauté, notamment l’usage d’une langue commune. Toutefois une société dont tous les individus partageraient entièrement une seule et même culture ne saurait évoluer. L’analogie avec les sociétés d’insectes nous incite à penser que la moitié de l’héritage culturel doit typiquement être diversifié.

Lorsqu’une société se réorganise, comme la France en 1789, sa culture évolue. Des penseurs comme Condorcet ont, à cette époque, réfléchi au rôle de l’enseignement. Une de ses thèses est que l’éducation doit se borner à l’instruction, c’est-à-dire à l’apprentissage de faits solidement établis, admis par tous, indépendamment de toute idéologie. En bon révolutionnaire, il rejette l’éducation religieuse à l’école. Celle-ci doit rester laïque et respecter l’indépendance des opinions sinon, elle peut porter atteinte aux droits des parents. On retrouve bien la même idée que l’héritage culturel doit être transmis en partie par la société et en partie par la famille. L’héritage de la société correspond aux gènes de la reine des abeilles. L’héritage de la famille correspond aux gènes des faux-bourdons.

Aujourd’hui l’évolution a été si rapide qu’on ne sait plus ni quoi ni comment enseigner.  Avec les vidéos et les ordinateurs, les enfants n’éprouvent plus le besoin d’apprendre à lire, ni à compter. Les programmes du secondaire ne cessent d’être modifiés, tandis que le baccalauréat n’offre plus de débouchés. Notre système d’éducation nationale s’effondre. Les parents n’ayant plus le temps de s’occuper de leur progéniture, les enfants des plus pauvres restent sans éducation. Ceux des plus riches sont confiés à des écoles privées de plus en plus nombreuses.  Aux inégalités de richesses s’ajoutent les inégalités culturelles. L’unité culturelle de la France se délite au profit d’une culture européenne calquée sur celle des États-Unis.

(1) François Roddier.  Thermodynamique de l’évolution. Éditions Parole (2012).

Dans ma réponse aux derniers commentaires sur mon billet 77, je parle du néocortex. Le développement du néocortex, notamment le cortex préfrontal, nous distingue des grands singes avec lesquels nous partageons plus de 99% de nos gènes fonctionnels. Quelques gènes, bien ciblés par la sélection naturelle, nous en séparent. Ces quelques gènes nous ont permis non seulement d’éliminer d’autres espèces homo concurrentes mais aussi de décupler par la technique notre dissipation d’énergie et d’envahir toute la planète. On reconnait là l’aspect non-linéaire de l’évolution qui produit des effets disproportionnés, sans rapport avec leurs causes, aspect qui rend son étude difficile.

Dans mon commentaire, je qualifie le néocortex de cerveau rationnel, le siège de la raison. En mathématiques, le mot raison signifie justement proportion. On lie généralement le développement du néocortex à la formation des premières sociétés et à la nécessité de partager équitablement la nourriture en proportion du nombre d’individus. On sait en effet que le néocortex est lié aux activités sociales, notamment le langage. Il est lié aussi à la mémoire dite « mémoire de travail » qui permet le calcul mental. Ces facultés mentales ont permis le développement des mathématiques, outil indispensable à toute science.

Une particularité du cerveau humain, appelée néotémie, est de garder des caractéristiques juvéniles. Les mathématiques ont sans conteste un caractère ludique et leur développement est vraisemblablement lié à ce caractère. Le physicien est plus intéressé par l’application des mathématiques au monde qui nous entoure. La physique reste cependant très proche des mathématiques. Les deux se sont souvent développés de concert comme en physique mathématique, les mathématiques apportant alors la rigueur aux méthodes plus intuitives des physiciens.

Le physicien s’intéresse avant tout aux grandeurs mesurables qui sont un gage de précision, différentes mesures pouvant être comparées entre elles. Les concepts physiques ont été peu à peu étendus à la chimie puis à la biologie et aux sciences humaines, notamment par le biais de la statistique, une progression logique allant du simple au plus complexe.

Je montre dans mon livre (1) comment de génétique, l’évolution est devenue progressivement culturelle. Déterminé dès la naissance par ses gènes, le comportement d’un insecte ou d’un lézard n’évolue plus une fois atteint l’âge adulte. Au contraire, déterminé par sa culture, donc initialement par son éducation, le comportement d’un être humain continue à évoluer toute sa vie.

Personnellement, j’ai évolué dans l’ordre logique: mon premier livre, a été un livre de mathématiques. Son sujet: la transformation de Fourier, est un outil pour les physiciens. Le fait que Joseph Fourier ait développé cet outil pour résoudre l’équation de la chaleur est peut-être prémonitoire de mon intérêt qui a suivi pour la dissipation de l’énergie. Dès ma retraite, je me suis intéressé à la biologie. Mes dernières conférences portent aujourd’hui sur l’économie.

Ma démarche scientifique reste cependant une démarche de physicien. Mes lecteurs ont pu remarquer que j’utilise sans cesse le mot processus. En physique, on parle de processus lorsque des grandeurs physiques sont liées par des équations permettant de décrire leur évolution. Prenons comme exemple une masse attachée au bout d’un ressort. L’équation différentielle qui lie la position de la masse au temps montre que la masse va osciller sinusoïdalement. Elle permet de calculer la période des oscillations.

Il arrive que d’autres grandeurs physiques soient liées par exactement les mêmes équations. C’est le cas par exemple du courant électrique dans une bobine mise en série avec un condensateur. L’équation différentielle qui lie la charge du condensateur au temps est la même que dans l’exemple précédent. Elle montre que le courant électrique va lui aussi osciller et permet de calculer la période des oscillations. Un physicien dira qu’il s’agit du même processus. C’est beaucoup plus qu’une métaphore ou une analogie, parce que la comparaison est quantitative et porte sur des grandeurs mesurables. Le comportement est exactement le même, bien que les échelles de temps ou d’espace peuvent être extrêmement différentes.

En passant du simple au complexe, reconnaître que la monnaie se comporte comme un catalyseur montre que le formalisme de la cinétique chimique pourrait s’appliquer à l’économie. Il apparaîtrait alors clairement que l’évolution économique s’apparente à celle d’une réaction de combustion. Une démarche analogue m’a fait dire que les cycles économiques sont des cycles de machines thermiques. Pour ceux qui ont écouté ma conférence du 12 mars (voir billet 75), j’y ai montré qu’on peut décrire l’évolution de chacun de ces cycles à l’aide des mêmes équations. Un physicien dira encore qu’il s’agit du même processus.

J’ai largement décrit dans mon livre (1), comme dans ce blog, le processus de criticalité auto-organisée découvert par le physicien danois Per Bak. Cet auteur a montré que les extinctions d’espèces en sont une conséquence. Elles sont dues à l’incapacité des gènes à s’adapter à une évolution qui devient trop rapide. L’évolution de l’espèce homo sapiens étant devenue largement culturelle, l’homme peut s’adapter beaucoup plus rapidement au changement de son environnement. Toute adaptation a cependant des limites. Les effondrements de civilisation ont remplacé les extinctions d’espèces. Là encore, le physicien dira qu’il s’agit du même processus. Ce qu’on sait sur l’un de ces deux phénomènes nous aide à comprendre l’autre.

Tandis que les extinctions d’espèces affectent la transmission des gènes, les effondrements de civilisation affectent la transmission de la culture. Dans nos sociétés modernes, ce rôle est réservé à l’école. On doit donc s’attendre à ce qu’un effondrement de civilisation se manifeste d’abord par un effondrement du système scolaire, un sujet que je me propose d’aborder prochainement.