Les économistes souhaiteraient faire de l’économie une science exacte au même titre que les sciences physiques. Ils tentent pour cela d’établir des relations mathématiques entre des grandeurs mesurables. Malheureusement, le choix de ces grandeurs est très pauvre. Il semble se limiter à deux. L’une est le temps qui est clairement défini. L’autre est la monnaie dont l’unité, autrefois liée à l’étalon or, est aujourd’hui plutôt mal définie, et semble fluctuer de façon incontrôlable.
Nous avons vu qu’une société humaine est une structure dissipative. Elle est modélisable comme un réseau d’agents échangeant de l’information. D’un point de vue strictement économique, l’information échangée est la monnaie. Il semble qu’on ait là de quoi jeter les bases d’une véritable science économique. Peut-on appliquer les résultats d’Ulanowicz à l’économie?.
On se heurte d’emblée à un problème fondamental lié à la notion de structure dissipative. Par définition, celles-ci sont dans un état stationnaire, c’est-à-dire qu’elles n’évoluent pas. Malheureusement on s’intéresse justement à leur évolution. Comment faire? En dynamique des fluides, on suppose que l’évolution d’un cyclone est suffisamment lente pour qu’on puisse encore définir la température et la pression du gaz en chaque point. C’est ce qu’on appelle l’équilibre thermodynamique local. Lorsqu’on mesure l’état d’un écosystème, on suppose implicitement que cet état ne varie pas sensiblement durant le temps des mesures. L’hypothèse apparait valable compte tenu de la précision des mesures. Qu’en est-il de l’économie?
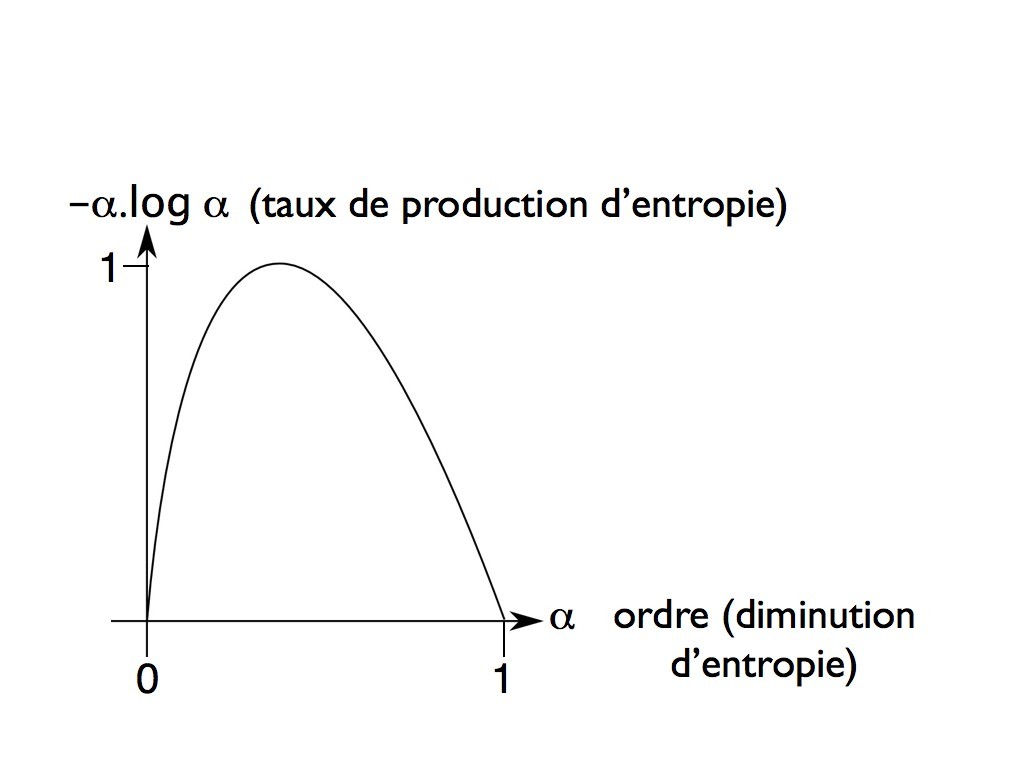
Les économistes résolvent généralement le problème en définissant l’état d’une économie sur l’échelle d’une année. Ce choix naturel permet de moyenner les fluctuations saisonnières (mais peut poser des problèmes dans le cas très fluctuant de l’économie financière). Quelle serait donc l’équivalent du paramètre d’ordre α d’Ulanowicz? Si l’on définit l’information comme étant donnée par la monnaie, alors l’information mémorisée est le capital. Cette information est en général mémorisée sur un compte bancaire. Normalisée au maximum égal à 1, c’est la fraction α du revenu annuel qui est capitalisée en vue de rapporter l’année suivante.
La quantité α est une variable aléatoire dont la réalisation n’est connue qu’à la fin de l’année i. L’expression d’Ulanowicz montre que α(i) peut aussi être considéré comme un estimateur bayésien (1) de la probabilité de profit pour l’année i+1. En ce sens, α(i) apporte pour l’année suivante une information α(i+1) qui vaut en moyenne α(i+1) = -α(i).log α(i). La quantité α(i+1) est ce qu’on appelle le revenu du capital. Les économistes la mettent sous la forme α(i+1) = r.α(i) où r est le rendement du capital. On voit que l’expression d’Ulanowicz implique un rendement du capital de la forme r = -log α. Cela peut paraître surprenant car il est infini à l’origine. Nous allons voir que c’est effectivement le cas.
Si l’on réinvestit chaque année le revenu du capital, on a ce qu’on appelle un revenu d’intétêts composés caractéristique des processus autocatalytiques. Une fois réinvesti le revenu du capital devient un nouveau capital α(i+1) = r.α(i), terme d’une progression géométrique de raison r. Il s’agit bien d’une cascade d’événements typique des processus d’auto-organisation. On sait que ces cascades sont déclenchées par des fluctuations aléatoires, ici des pertes ou des gains accidentels en moyenne nuls. Un gain de moyenne nulle peut être considéré comme un revenu accidentel sans capital. Son rendement est bien infini. Lorsque ce gain est investi, il peut engendrer une cascade plus ou moins importante d’événements capables de créer des fortunes. C’est la base du système capitaliste, souvent qualifié de « rêve américain », dans lequel n’importe qui est sensé pouvoir devenir riche.
L’expression d’Ulanowicz implique qu’il existe une valeur critique α = 1/e (37%) pour laquelle la raison r = -log α de la progression est égale à l’unité. Le revenu du capital compense alors tout juste les dépenses et maintient le capital constant. Lorsque α < 1/e, la raison r de la progression est supérieure à l’unité, de sorte que le capital croit chaque année. Dans le cas d’un pays, on parle de croissance économique. Lorsque α > 1/e, la raison r de la progression devient inférieure à l’unité et le capital décroit. Lorsqu’il y a eu création monétaire, c’est-à-dire que le capital a été emprunté à une banque, alors il ne peut plus être remboursé et c’est la faillite, d’où la terreur des économistes à l’idée d’une décroissance économique.
Tout système économique, nation ou entreprise, cherche à maximiser le revenu de son capital de façon à faire croître ce dernier. On voit qu’il y a une limite au delà de laquelle le capital ne croit plus et même décroit, c’est le point critique caractérisé par le nombre sans dimension 1/e. Il semblerait que l’on puisse généraliser ce résultat à toute structure dissipative (2). Celle-ci va s’adapter à son environnement de façon à maximiser l’information reçue jusqu’au moment ou l’information qu’elle mémorise ne croit plus et même décroit. Elle a alors atteint le point critique. Elle mémorise alors autant d’information qu’elle en efface. Cela implique que le point critique est aussi un point de dissipation maximale d’énergie. On sait qu’une structure dissipative oscille constamment autour du point critique en quête du maximum (billet 21).
(1) Un estimateur bayésien (ou inférence bayésienne) estime la probabilité d’un événement à partir de celles d’événements précédents.
(2) Considérée comme un réseau d’agents échangeant de l’information.
Bonjour,
Et bravo pour vos publications et conférences : passionnants !
Pourriez-vous rajouter un bouton sur votre blog pour tweeter ou publier vos articles sur les principaux réseaux ?
Cela permettrait de faire un peu de buzz sur vos travaux.
Merci,
Eric
Bonjour monsieur Roddier
Merci pour cet excellent article, je me pose une question.
Et si la limite du capitalisme était son approvisionnement énergétique fossile.
Il semblerait quand même qu’on peut avancer que moins d’énergie fossile serait comparable à moins d’informations dans le système.
Un excellent article sur le blog de Matthieu Auzzaneau concernant le sujet et d’ailleurs, il vous cite.
http://petrole.blog.lemonde.fr/2016/02/11/2015-risque-detre-lannee-du-pic-petrolieret-des-limites-physiques-de-la-croissance/#more-12193
Bonjour,
encore un très bon article!
On reconnait dans le processus que vous décrivez tout les ingrédients de « l’effet de la reine rouge ».
La recherche de croissance ad infinitum à pour conséquence d’entrainer un ensemble de retro-actions demandant une exploitation sans cesse décupler des ressources planétaire , d’où l’écocide contemporain à laquelle nos élites veulent faire face par plus de… croissance!
Cordialement.
Ma remarque sera plutôt d’ordre général et je reposte ici ma remarque initiale ( voir post 80 : la notion de processus) pour commencer une série de remarques générales :
Bien sûr je rends d’abord hommage à votre intelligence et à la simplicité limpide de vos explications.
Maintenant, ma remarque. Vous voudrez bien me reprendre si je commets une erreur :
la démarche mathématique à la base de la Physique et des extensions fort intéressantes que vous proposez à des domaines vivants possède une faille constitutive si on interprète Gödel comme suit :
en effet, pour ce Logicien, les théories mathématiques possédant axiomatiquement l’Arithmétique ( c’est à dire toutes celles auxquelles vous faites référence dans ce blog) sont : soit incomplètes (indécidables localement), soit contradictoires (absurdes).
Ce fait résulterait du fameux théorème d’incomplétude portant son nom.
Cette faille est comme un accroc dans un tricot : on peut très bien ne pas le remarquer, voire l’ignorer. Mais l’usage de la théorie peut très bien finir par tout réduire en charpie (au niveau du réel cette fois).
Le problème scientifique majeur reste toutefois l’absence de fondement rationnel à tous ces développements; même si il ne s’agit que d’imperfections logiques d’apparence mineure, la rigueur mathématique, en tous cas logique, entraîne leur caducité. Ne pas en tenir compte, autrement dit ne pas repartir hors des moyens arithmétiques, est une réalité sociale ancrée ( un puits de potentiel ?). Cela n’en n’est pas moins un passage de la science ( et de la philosophie) au sophisme voire au religieux, version 2.0.
Cette croyance aussi doit s’effondrer. Tôt ou tard.
J’espère que nous aurons l’occasion d’approfondir cette question.
A bientôt de vous lire.
Eric Basillais
Et bien, lorsqu’il n’y a plus de croissance possible, du fait de la raréfaction des ressources, soit :
– on les trie ;
– on les crée ;
– on se porte sur les idées, la culture ;
Car il est probable qu’en détruisant l’environnement, nous ne faisions en fait que de nous détruire.
L’environnement a son temps de récupération, qui semble être un invariant.
Merci beaucoup, c’est fait.
Ne confondez pas énergie et information. L’humanité a besoin d’informations pour développer de nouvelles sources d’énergie.
Le temps de récupération dépend de l’amplitude des dégâts, d’où la loi en 1/f.
Bonjour Je suis en train de lire votre « thermodynamique de l’évolution », qui est passionnante. Je me demande si , pages 82 et 83 il n’y aurait pas une coquille en 8.5 dans les trois types d’eucaryotes distingués par leur métabolisme. Ne serait-ce pas photoautotrophes utilisant l’énergie solaire (au lieu d’autotrophes) et autrophes utilisant des déchets organiques (au lieu d’hétérotrophes déjà défini dans la même phrase comme se nourrissant de matière vivante). Merci pour vôtre capacité à rendre claires des règles complexes qui éclairent ce que nous sommes.
Les organismes autotrophes peuvent se nourrir uniquement de matière minérale (exemple: les plantes). Les organismes hétérotrophes ont besoin de matière organique, soit fraiche (exemple: les animaux), soit putréfiée (exemple: les champignons).
Dans un système fermé comme le capitalisme industriel, l’entropie augmente, l’information disparaît et le système va vers l’équilibre thermodynamique, la mort en ce qui concerne les sociétés humaines.
Ceci dit, la culture de ce système a créé une quantité importante d’informations qui peuvent être utilisées pour créer de nouvelles sources d’énergie à partir du renouvelable et elle va surtout créer une quantité d’informations quand à la façon efficace de les utiliser.
Il me semble qu’après la culture industrielle il va falloir inventé (si on peut inventer une culture) une culture du biomimétisme.
bonjour,
Si la monnaie est une information, donc une énergie, alors les banques centrales qui ont le pouvoir d’en créer autant qu’elles le souhaitent — quitte à acheter à des prix exorbitants de vieux vélos rouillés comme « actifs » en contrepartie de la monnaie-dette créée à cette occasion dans leur bilan. Elles peuvent donc créer autant d’énergie qu’elles le souhaitent : l’humanité est sauvée !
…à moins que la thermodynamique ne les rappelle à l’ordre ?
En économie on parle plutôt de signal-prix, c’est-à-dire que les prix sont l’information, pas la monnaie (il peut d’ailleurs n’y avoir aucune transaction monétaire alors que les prix sont disponibles). En pratique l’un et l’autre sont liés par une boucle de rétroaction selon une relation fluctuante et imprécisément connue.
La manipulation, aujourd’hui éhontée, de leur monnaie par les banques centrales affecte la monnaie et les prix. Ils perdent leur signification. Ainsi l’énergie ou l’information associées perdraient leur substance, ce qui n’est pas concevable en physique. Ne pourrait-on en déduire une mesure de la santé d’une monnaie ? ou les « véritables » prix ? Comment la thermodynamique pourrait-elle dévoiler ces « villages Potemkine » monétaires ?
J’ai hâte de recevoir l’exemplaire de votre livre que j’ai récemment commandé.
Certaines religions honnissent le prêt à intérêt dans leurs textes sacrés (la réalité étant autre chose…). Elles prescrivent aussi le jeûne.
A votre avis, ont-elles compris que l’homme devait arrêter d’osciller sans cesse autour de 1/e ? (guerres, révoltes…)
Un discours religieux est-il orienté vers la recherche du maximum 1/e ?
non pas pour contribuer, mais pour transmettre un zeste de religiosité ou de philosophie, voici une approche tout aussi brillante de la monnaie, une équation philosophique : http://blogs.lecho.be/colmant/2016/04/la-monnaie-avec-un-zeste-biblique-.html#ixzz45h6pMwxK
c’est le blog de Bruno Colmant.
Soit PIB = Y = C + I (secteurs privé et public confondus)
–> par :
« Si l’on définit l’information comme étant donnée par la monnaie, alors l’information mémorisée est le capital. Cette information est en général mémorisée sur un compte bancaire. Normalisée au maximum égal à 1, c’est la fraction α du revenu annuel qui est capitalisée en vue de rapporter l’année suivante. »
voulez-vous dire que 1 = C/Y + α ?
α = 1/e = 37% et r = -log α = 43%
Or le ROI attendu par les actionnaires majoritaires s’élève en moyenne à 8 % pour les entreprises cotées :
https://fr.wikipedia.org/wiki/Retour_sur_investissement
–> le taux de 43% est-il réaliste ?
À moins que par :
« L’expression d’Ulanowicz implique qu’il existe une valeur critique α = 1/e (37%) pour laquelle la raison r = -log α de la progression est égale à l’unité. »
Vous voulez dire que :
soit r = -ln α
alors la valeur de α pour laquelle r = 1 est telle que
1 = – ln α α = 1/e
C’est bien celà ?
ERRATUM :
alors la valeur de α pour laquelle r = 1 est telle que
1 = – ln α ⇔ α = 1/e
Vous semblez oublier qu’entretenir sa maison (si vous en possédez une) ou acheter une nouvelle voiture est aussi un investissement.