En dessous d’une certaine température et d’une certaine pression dites “critiques”, un fluide homogène peut devenir spontanément inhomogène. Il se décompose alors en deux “phases”, une phase liquide et une phase vapeur. Bien que le fluide soit en équilibre thermodynamique, ce processus est formellement équivalent à celui d’une bifurcation d’une structure dissipative (les équations sont analogues). Le point où la pression et la température atteignent la valeur critique s’appelle le point critique. En ce point les fluctuations de densité du fluide deviennent théoriquement infinies. On dit alors que le fluide est dans un état critique.

Spécialiste des états critiques, le physicien danois Per Bak s’est intéressé aux bifurcations des structures dissipatives pour lesquels les points de bifurcation jouent le rôle de point critique. En 1987, Per Bak a montré que certaines structures dissipatives évoluent de façon à toujours se rapprocher d’un point de bifurcation. En ce point on dit que la structure dissipative est dans un état critique. En 2002, Roderick Dewar a montré que cette propriété est une conséquence du principe de production maximale d’entropie lorsqu’une structure dissipative est soumise à un apport d’énergie dont le flux est limité, ce qui est très souvent le cas.

Jusqu’ici nous avons décrit les propriétés d’une structure dissipative en observant le flux d’énergie pour une tension donnée. Mais comment évolue la tension? Pour le voir, nous allons reprendre l’exemple de la suite logistique décrit dans l’article précédent (article 20). Le flux d’énergie y est proportionnel au nombre d’individus, c’est-à-dire à la valeur de la population. La figure de l’article précédant montre cette valeur en fonction du taux de croissance. Le principe de production maximale d’entropie nous indique que le flux d’énergie va tendre a être maximal. Cela veut dire que la population va tendre à augmenter jusqu’à atteindre une valeur maximale compatible avec les contraintes imposées, ici des ressources énergétiques limitées. On voit que ce maximum est effectivement atteint au voisinage du premier point de bifurcation, après lequel la valeur de la population devient instable et oscille. Pourquoi cela? Est-ce là une loi générale?

Pour comprendre ce phénomène, nous allons reprendre notre analogie du flux d’énergie avec le flux d’une rivière (article 19). Nous avons vu que l’énergie est constamment piégée dans des puits de potentiel. L’analogie sera pour nous des réservoirs d’eau souterraine (puits d’eau). Pour extraire de l’énergie d’un puit de potentiel, il faut un apport minimum d’énergie appelé énergie d’activation (article 12). A l’échelle moléculaire cette énergie peut être fournie par une collision (entre molécules) ou par un catalyseur (molécule jouant le rôle de batterie rechargeable). A notre échelle, ce sera par exemple l’énergie apportée par une alumette capable d’allumer un incendie. Dans le cas d’une entreprise, nous parlerons plus tard d’investissement. Dans tous les cas, l’énergie extraite du puits est bien supérieure à l’énergie d’activation.

Pour notre puits d’eau souterraine, l’analogue sera un siphon. L’énergie d’activation est celle nécessaire pour amorcer le siphon. Dans une telle structure, le niveau d’eau (qui joue ici le rôle de tension ou stress) augmente jusqu’à ce que le siphon s’amorce. C’est l’instabilité qui entraîne une restructuration (bifurcation): celle-ci permet à l’eau de s’écouler. Le réservoir se vide d’un seul coup, le siphon se désamorce et le cycle recommence. Il y a effectivement oscillation. Ce type d’oscillation non linéaire porte le nom d’oscillation de relaxation. On voit qu’une telle structure est effectivement attirée vers une bifurcation. Lorsque la bifurcation est franchie, l’énergie (ici l’eau) est libérée et tout recommence comme au début.

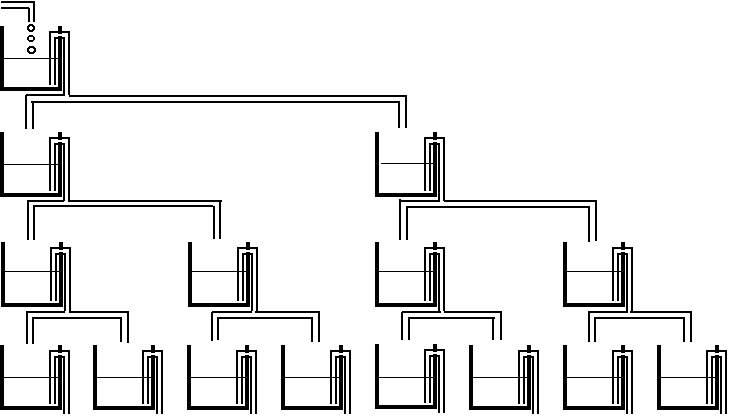
Nous avons vu que l’énergie de l’Univers est constamment redistribuée dans des puits de potentiel (ou niveaux d’énergie) de plus en plus nombreux, d’où l’augmentation constante de l’entropie (article 19). Imaginons une cascade de puits comme celle de la figure ci-dessous. Une telle structure présente toute une arborescence de bifurcations. Dans cet exemple, le nombre de puits double à chaque niveau.

Analogie hydraulique d’une cascade de puits de potentiel

Le premier puits est alimenté par un flux d’eau constant et se remplit lentement. Supposons qu’il faille une minute pour remplir le premier puits. Au bout d’une minute, il se déverse dans les deux puits suivants, les remplissant à moitié. Au bout d’une deuxième minute, le premier puits est à nouveau plein. En se déversant, il achève de remplir les deux puits suivants. Ceux-ci se déversent alors dans les quatre puits suivants. Au bout de quatre minutes, ceux-ci sont pleins à leur tour et se déversent dans les huit puits suivants, etc… On observe ainsi des avalanches de plus en plus importantes (un, deux, quatre, huit puits, …) à des intervalles de temps de plus en plus longs (une, deux, quatre, huit minutes, …).

Remarquons que chaque étage se déverse à tour de rôle au moment précis où tous les étages précédents viennent de se déverser. Dans le cas de la figure où tous les puits sont représentés à moitié pleins, tous les étages vont se vider dès que le premier le fera. Il y a donc une réaction en chaîne provoquant une cascade d’avalanches à tous les niveaux. On appelle cela l’effet domino. Un domino posé sur la tranche peut en tombant faire tomber tous ses voisins. De même, en se vidant un puits peut entraîner un certain nombre de puits suivants à se vider eux aussi.

C’est ce que Per Bak appelle une suite d’états critiques auto-organisés (self-organized criticality ou SOC). Une caractéristique de ce genre de phénomène est qu’on observe des bouffées d’énergie (avalanches) d’autant plus fréquentes que leur amplitude est plus faible. On dit que la fréquence des avalanches est inversement proportionnelle à leur amplitude, ou encore que l’amplitude des avalanches est inversement proportionnelle à leur fréquence. C’est ce que les physiciens appellent un “bruit en 1/ f “. Son importance vient du fait qu’on l’observe très souvent, non seulement en électronique, mais aussi en astronomie, en géophysique, en biologie et même en économie.

Dans notre exemple très simple d’un réseau régulier de puits de potentiel tous identiques, les avalanches sont parfaitement prédictibles. En pratique, les structures naturelles sont beaucoup plus irrégulières. Les puits n’ont pas tous la même capacité. Les siphons s’amorçent aléatoirement. La redistribution à chaque étage est elle-même aléatoire. Dans ce cas, les avalanches sont imprédictibles, mais elles suivent bien la loi en 1/ f que nous venons de voir.

Le modèle plus réaliste proposé par Per Bak est celui du tas de sable. Imaginons du sable tombant en pluie fine sur une table. Un tas de sable se forme dont la pente augmente peu à peu pour atteindre une pente critique au delà de laquelle le sable s’écoule puis tombe en dehors de la table. On est alors en régime permanent. Ce régime est caractérisé par des avalanches de sable imprévisibles mais dont la fréquence est bien inversement proportionelle à l’amplitude.

Remarquons que dans les deux exemples que nous avons donné, le phénomène observé est indépendant de la taille de la structure, par exemple la taille du tas de sable. On y retrouve l’invariance par changement d’échelle décrite dans l’article 18, c’est-à-dire des cascades d’énergie obéissant à des lois de puissance. D’une façon générale l’auto-organisation des états critiques se traduit par des restructurations partielles aléatoires d’autant moins fréquentes que la restructuration est plus importante.

Depuis la mise en évidence de ce processus par Per Bak, on en découvre régulièrement de nouveaux exemples. Nous en décrirons certains dans notre prochain article. On se contentera ici de dire que le processus peut s’appliquer à l’évolution d’une population en présence de ressources limitées. Le modèle analytique de la suite logistique est trop simple pour décrire correctement la réalité. Les oscillations régulières qu’il prévoit n’ont jamais été observées. Par contre, on observe effectivement des chutes brutales de la densité de population provoquées par des disettes, des épidémies ou —chez l’homme— des guerres. Ces chutes de densité sont d’autant plus fréquentes que leur amplitude est plus faible. Très rarement, une chute de très grande amplitude peut avoir lieu (effet domino) expliquant des phénomènes comme la fin de l’île de Pâques, ou ceux décrits au début de cette série d’articles (articles (1) et (2)). Nous verrons qu’on a là un modèle extrêmement fécond pour comprendre l’évolution des sociétés humaines.

Liens internet:
Point critique (en français):
http://fr.wikipedia.org/wiki/Point_critique_%28thermodynamique%29
Biographie de Per Bak (en anglais):
http://en.wikipedia.org/wiki/Per_Bak
Bruit en 1/f (en français):
http://gilles.chagnon.free.fr/cours/courlong/4_4_2_3.html
Références sur le bruit en 1/f (en anglais):
http://www.nslij-genetics.org/wli/1fnoise/
Etats critiques auto-organisés (en anglais):
http://en.wikipedia.org/wiki/Self-organized_criticality
Exemple du tas de sable (en français):
http://www-eco.enst-bretagne.fr/~phan/complexe/sable.htm
Livre:
Per Bak, How Nature Works: The Science of Self-Organized Criticality (Springer-Verlag, 1999).