Revenons aux notions de thermodynamique élémentaire que nous avons introduites à l’article 6. L’énergie mécanique peut être intégralement convertie en chaleur, une forme d’énergie associée au mouvement microscopique désordonné des molécules. Mais la chaleur ne peut être que partiellement convertie en travail mécanique. Elle ne peut l’être qu’en présence de différences de températures, c’est-à-dire de variations d’un paramètre macroscopique observable et contrôlable, la température.

Cela a amené l’américain J. Willard Gibbs à distinguer deux sortes d’énergie, l’énergie libre et l’énergie liée. L’énergie libre, entièrement convertible en travail mécanique, est celle associée aux paramètres macroscopiques de l’espace des phases décrit dans notre précédent article. Par opposition, l’énergie liée est celle associée aux paramètres microscopiques inobservables. Lorsqu’on mélange de l’eau chaude et de l’eau froide, les différences de température initiales s’estompent. Il y a bien conservation de l’énergie, mais l’énergie libre associée à des différences macroscopiques de température se transforme irréversiblement en énergie liée, associée au mouvement microscopique inobservable et incontrôlable des molécules. Les thermodynamiciens expriment ce fait en disant que l’entropie du mélange a augmenté.

On comprend ainsi la relation découverte par Claude Shannon entre l’entropie et l’information (article 8). Le transfert d’énergie de paramètres observables à des paramètres inobservables se traduit en effet par une perte d’information. Comme il y a augmentation d’entropie, cela veut dire qu’un gain d’entropie est l’équivalent d’une perte d’information. Cette équivalence entre information et entropie (ou plutôt son opposé appelé négentropie) paraît maintenant claire. Elle pose cependant un problème car l’information telle que Shannon l’a définie (voir article 8) est liée à la notion de probabilité.

Pour un physicien toute grandeur physique est nécessairement une quantité objective, c’est-à-dire indépendante de l’observateur. Le problème est alors de savoir si une probabilité peut être considérée comme une quantité objective. C’est malheureusement difficilement le cas. Lorsqu’un météorologue estime la probabilité de beau temps, il fonde ses prévisions sur un ensemble d’observations ayant une précision limitée. Cela entraîne qu’un observateur différent fera des prévisions peut-être similaires à court terme mais qui pourront devenir très différentes à long terme. La probabilité dépend donc de l’observateur.

Le problème vient du fait qu’on est en présence d’information incomplète. Le physicien américain E. T. Jaynes a montré que cela n’empêchait pas de raisonner objectivement. Pour cela on part d’une probabilité à priori qui est effectivement “subjective” dans la mesure où deux observateurs différents disposent d’observations différentes et on l’affine au fur et à mesure que de nouvelles observations deviennent disponibles. On obtient ainsi une probabilité à posteriori de plus en plus objective. C’est ainsi que la science progresse. La méthode générale pour y parvenir porte le nom d’estimation bayesienne du nom du mathématicien et pasteur anglais Thomas Bayes.

Le fait que l’entropie dépend de l’information à priori que possède l’observateur apparaît clairement dans ce qu’on appelle le paradoxe de Gibbs. Considérons une enceinte isolée formée de deux compartiments séparés par une cloison amovible. Initialement, ces deux compartiments contiennent de l’oxygène gazeux à la même température et à la même pression. Il y a équilibre thermodynamique. L’expérimentateur retire alors la cloison en la faisant lentement glisser parallèlement à elle-même sans fournir de travail mécanique. Il y a toujours équilibre thermodynamique. L’état macroscopique du gaz n’a pas changé. Son entropie est restée la même.

L’expérimentateur apprend alors que les compartiments contenaient deux isotopes différents (1). L’un contenait de l’oxygène 16, l’autre de l’oxygène 18. Lorsqu’il a retiré la cloison ces deux isotopes se sont mélangés. Cette transformation étant irréversible, l’entropie du gaz a augmenté. La variation d’entropie est finie et aisément calculable. Dans le premier cas les molécules d’oxygène étaient considérées par l’observateur comme indiscernables. Dans le second cas, elles sont considérées comme discernables. La variation d’entropie dépend donc de la connaissance à priori qu’a notre observateur sur le gaz et de sa capacité à en discerner les molécules.

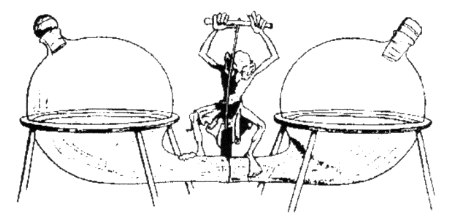
Le fait que l’entropie a un aspect subjectif n’avait pas échappé au physicien écossais James Clerk Maxwell. Celui-ci avait en effet entrevu une possibilité de mettre en défaut le second principe de la thermodynamique. Imaginons à nouveau une enceinte isolée formée de deux compartiments séparés par une cloison. Les deux compartiments contiennent le même gaz à la même température et à la même pression. La cloison est percée d’un petit orifice capable de laisser passer une molécule à la fois. Maxwell imagine un “démon” capable de contrôler le passage à travers l’orifice en faisant glisser une cloison, toujours sans travail mécanique (figure ci-dessous).

Le démon de Maxwell (2)

Il laisse par exemple passer les molécules rapides vers la droite mais pas vers la gauche et laisse passer les molécules lentes vers la gauche mais pas vers la droite. Il peut ainsi faire naître une différence de température entre les deux compartiments ce qui est bien contraire au second principe. Pour reprendre notre exemple précédent, ce même démon pourrait tout aussi bien séparer ainsi l’oxygène 16 de l’oxygène 18. De façon générale, il est capable de diminuer l’entropie d’un système isolé ce que le second principe ne permet pas.

Il doit cette prouesse à sa capacité d’observer et de contrôler des paramètres à l’échelle microscopique. Comme l’a montré le physicien français Léon Brillouin la diminution d’entropie du gaz correspond très exactement à la quantité d’information collectée par le démon et enregistrée sous la forme d’un changement d’état du gaz. En diminuant l’entropie de ce système, il rend possible la production de travail mécanique. Par exemple, il peut permettre à un moteur thermique de fonctionner à partir des différences de températures qu’il aura ainsi créée.

C’est un fait général que toute collecte d’information entraîne une diminution d’entropie donc une “libération” d’énergie susceptible de se dissiper. Ce fait a des conséquences considérables. La suite de ce blog sera consacrée à leur examen.

(1) Un même élément chimique peut avoir des atomes de masses différentes parce contenant un nombre de neutrons différent. Ainsi l’atome d’oxygène 18 contient deux neutrons de plus que l’atome d’oxygène 16.
(2) Dessin tiré de Darling & Hulburt, American Journal of Physics, 23-7, 1955.

Liens internet:
http://en.wikipedia.org/wiki/Josiah_Willard_Gibbs
http://fr.wikipedia.org/wiki/Énergie_libre
http://fr.wikipedia.org/wiki/Claude_Shannon
http://en.wikipedia.org/wiki/Edwin_Thompson_Jaynes
http://fr.wikipedia.org/wiki/Thomas_Bayes
http://fr.wikipedia.org/wiki/Paradoxe_de_Gibbs
http://fr.wikipedia.org/wiki/James_Clerk_Maxwell
http://fr.wikipedia.org/wiki/Démon_de_Maxwell
http://fr.wikipedia.org/wiki/Léon_Brillouin