Au cours des articles précédents, nous avons vu que l’Univers évolue en dissipant de plus en plus d’énergie. La dissipation se fait par l’intermédiaire de structures dissipatives (article 17). Celles-ci évoluent et sont peu à peu remplacées par de nouvelles structures toujours plus efficaces que les précédentes. C’est ainsi que sont apparues des structures dissipatives particulièrement efficaces: les êtres vivants. Plus efficace que les autres, l’homme a envahi la planète, formant des sociétés capables de dissiper plus d’énergie par unité de masse que toute autre structure de l’Univers (article 18).
Nous verrons que plus une structure dissipative dissipe de l’énergie, plus vite elle évolue et plus tôt elle doit se restructurer. Nous avons appelé ces restructurations des bifurcations (article 20). Dans l’article précédent (article 21), nous avons vu qu’une bifurcation peut en entraîner beaucoup d’autres. On observe alors des cascades de bifurcations. Ces cascades sont d’autant plus rares qu’elles sont plus importantes. Des bifurcations isolées ou de petites cascades sont très fréquentes. Plus rarement, on assiste à de véritables avalanches ou cataclysmes. La fréquence des cascades dépend de leur amplitude suivant une loi de puissance caractéristique des processus invariants par changement d’échelle (article 18). La loi est en général proche d’une loi en 1/ f (article 21). En voici quelques exemples (Voir: Turcotte et al. 2002).
C’est le cas bien sûr des avalanches naturelles, analogues à celles des tas de sable. Lorsque la pente est suffisante, une pierre qui roule peut en entraîner plusieurs. Chacune de ces dernières va à son tour en entraîner d’autres. Le processus est semblable à celui des cascades décrites dans l’article précédent. Au lieu d’une avalanche d’eau, on a une avalanche de pierres. A partir de photographies aériennes, on peut compter les avalanches produites par un tremblement de terre et mesurer leur importance c’est-à-dire leur surface. En général, leur nombre est bien inversement proportionnel à leur surface (loi en 1/ f). C’est le cas aussi des avalanches déclenchées par la pluie ou la neige.
Un second exemple est donné par les tremblements de terre. Une quantité importante d’énergie, dite géothermique, est emprisonnée à l’intérieur du globe terrestre et cherche à se dissiper. Elle le fait par l’intermédiaire de mouvements convectifs dans le manteau supérieur. Ceux-ci poussent les unes contre les autres les plaques solides de la croûte terrestre. C’est la dérive des continents appelée aussi tectonique des plaques. Les plaques résistent à cette compression en se déformant lentement (régime linéaire élastique). La tension augmente (comme celle d’un ressort qu’on comprime) jusqu’au moment critique où la limite d’élasticité est dépassée. Cela produit une rupture locale de la roche.
Cette rupture peut en déclencher d’autres. On observe alors toute une série plus ou moins longue de ruptures en cascade. C’est le tremblement de terre ou séisme. Les séismes sont enregistrés par les sismographes. Les sismographes enregistrent des séismes tous les jours mais la plupart ne sont pas ressentis par les humains. L’importance (ou magnitude) d’un séisme se mesure sur l’échelle de Richter. Seuls les plus importants d’entre eux sont ressentis par les humains. Certains, extrêmement puissants mais heureusement rares, provoquent les catastrophes naturelles très destructrices que l’on connait.
La fréquence des séismes est d’autant plus faible que leur importance est plus grande. Si l’on porte sur une échelle logarithmique le nombre de séismes de magnitude supérieure à une certaine valeur en fonction de cette valeur, les points sont en général remarquablement alignés. C’est la loi de Gutenberg-Richter. La figure ci-dessous montre un exemple tiré d’une statistique des séismes sur la côte ouest du Canada. Elle montre que la fréquence des seismes suit une loi en 1/ f. (Voir le site Ressources naturelles Canada).
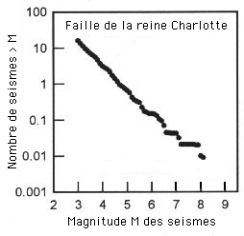
|
| Loi en 1/f de fréquence des séismes |
Un troisième exemple est donné par les feux de forêt. Il arrive que, lors d’un orage, un arbre prenne feu. Si la forêt est suffisamment dense, le feu peut s’étendre aux arbres voisins. En brûlant, ceux-ci peuvent à leur tour communiquer l’incendie à leurs voisins. On a, là aussi, un phénomène de cascades allumant des brasiers de plus en plus nombreux. Lorsqu’on compte le nombre de feux de forêt d’extension donnée en fonction de cette extension, on trouve encore une loi en 1/ f.
On passe aisément des feux de forêt aux épidémies. Un individu infecté risque de contaminer ses voisins qui risquent eux-mêmes de contaminer d’autres personnes. Des statistiques ont été faites sur la fréquence des cas de rougeole, coqueluche et oreillons dans des sociétés insulaires (voir: Rhodes et al., 1997). Là encore, la loi en 1/ f est vérifiée. A l’échelle du globe, on observe en général plusieurs pandémies (plus de 10 millions de morts) par siècle. Quoique plus rares, des pandémies encore plus graves sont donc loin d’être exclues.
Ceci nous amène au problème de l’extinction des espèces. Jusqu’à récemment, on pensait que l’évolution des espèces était progressive, les caractéristiques des individus se modifiant peu à peu au cours des millénaires. Or, la paléontologie montre une absence de variations notables des fossiles pendant de longues périodes, précédées ou suivies immédiatement par des périodes de fossiles très différents.
Pendant longtemps ce phénomène a été interprété comme dû à des lacunes dans les échantillons paléontologiques, liées à des irrégularités de nature purement statistique. En 1972, les paléontologistes Stephen Jay Gould et Niles Eldredge ont émis l’hypothèse, dite des équilibres ponctués, selon laquelle ce phénomène était bien réel et significatif. Critiquée par des zoologistes comme Richard Dawkins, cette hypothèse a fait l’objet de débats télévisés connus pour avoir donné aux créationistes américains l’occasion de mettre en doute la théorie de Darwin.
En 1993, Bak et Sneppen ont montré que les équilibres ponctués étaient vraisemblablement un processus d’auto-organisation d’états critiques. On sait que l’évolution des espèces est due à des mutations. Jusqu’ici, on pensait qu’elle était due à toute une suite de mutations successives produisant chacunes de petites variations. D’après Bak et Snappen, on néglige ainsi les interactions entre espèces.
Une petite variation d’une espèce doit être considérée comme un changement d’environnement pour une autre espèce. Elle peut donc modifier l’aptitude à survivre des individus de cette autre espèce et par suite influencer leur évolution. En évoluant, ceux-ci vont à leur tour modifier l’évolution d’espèces encore différentes. On retouve ainsi le phénomène de cascades dont nous avons donné de nombreux exemples.
Les simulations numériques montrent bien des effets semblables à ceux observés par les paléontologistes. On aurait de temps à autre des avalanches plus ou moins importantes d’extinctions brutales. Ainsi l’évolution des espèces serait en fait une cascade de bifurcations et l’arbre des espèces, une arborescence de bifurcations. Le développement que l’on croyait progressif chez l’homme du geste et de la parole (voir: Leroi-Gourhan) apparait depuis peu lié à une floraison d’espèces “homo” toutes différentes, c’est-à-dire à tout un enchaînement de bifurcations.
Le processus d’auto-organisation d‘états critiques est maintenant pris très sérieusement en considération en biologie. Un certain nombre de chercheurs pensent qu’il s’applique aussi en sociologie (voir Hanson, 2007) et qu’il explique des phénomènes comme l’effondrement des sociétés décrit par Jared Diamond. Nous reviendrons largement sur ce sujet.
Références et liens internet:
Donald L. Turcotte et al., Self-organisation, the cascade model, and natural hasards, PNAS, vol. 99 Suppl. 1, 2530-2537, feb. 2002, accesible à:http://www.pnas.org/cgi/content/full/99/suppl_1/2530
Tectonique des plaques http://fr.wikipedia.org/wiki/Tectonique_des_plaques
Echelle de Richter
Allumez vous-mêmes vos feux de forêt:
http://argento.bu.edu/java/java/blaze/blazeapplet.html
C. J. Rhodes, H. J. Hensen and R. M. Anderson, On the critical behaviour of simple epidemics, Proc. R. Soc. Lond. 264, 1639-1646, 1997, accessible à: http://www.journals.royalsoc.ac.uk/content/c1pyphnvew7q8mcg/fulltext.pdf
Faites évoluer votre propre écosystème:
http://perso.univ-rennes1.fr/denis.phan/complexe/pap/baksnep.html
Robin Hanson, Catastrophe, Social Collapse, and Human Extinction, January 2007) accessible à: http://hanson.gmu.edu/collapse.pdf
Le modèle de Per Bak et Kim Sneppen (« Punctuated equilibrium and criticality in a simple model of evolution », « Evolution as a self-organized critical phenomenon »), ou, plus généralement, le point de vue qu’ils adoptent, montre que le terme « adaptation » et le vocable « sélection des plus aptes », trop généralement utilisés, sont très ambigus. Lorsque chaque espèce est adaptée à une niche écologique, la tendance à l’évolution se ralentit. Les mutations génétiques, au hasard de la réplication d’ADN, sont soit indifférentes, soit défavorables aux individus qui les portent. Et, quand elles sont favorables, elles sont trop faibles pour permettre d’envahir la niche voisine (« barrière à l’entrée »), à laquelle l’espèce qui l’occupe est très adaptée. Dans ce contexte, la biosphère terrestre semble stable pendant une période assez longue. Un observateur, naïf ou extérieur (le Petit Prince venu de sa planète), se dit « tout cela est statique, prévu de toute éternité par une intelligence qui a tout prévu dans les moindres détails et pour l’éternité. Quelle harmonie dans la Création ». Mais il suffit d’une petite accumulation de petites mutations à petit bruit pour que, dans chaque niche, chaque espèce qui a accumulé des petites « fragilités », devienne plus sensible à une modification quelconque du contexte, local ou global. La biosphère terrestre qui semble parfaite et harmonieuse (comme l’équilibre des économistes, qui est aussi un optimum), peut entrer, d’abord à petit bruit, dans un déséquilibre qui peut conduire à une extinction d’espèces, voire à une extinction massive.
Leçon. Un terme mal adapté, employé par anthropomorphisme, par humour, par provocation ou par effet de mode, peut avoir des effets catastrophiques sur l’interprétation généralement admise d’une théorie scientifique, pourtant très pertinente. Combien de philosophes disent que le relativisme a été « démontré » par Einstein dans sa théorie de la Relativité ? Comme le dit Etienne Klein, les scientifiques doivent faire attention aux connotations du vocabulaire qu’ils emploient.