Les condensations successives qui ont eu lieu après le Big Bang m’amènent à parler aujourd’hui d’une notion très importante en mécanique statistique, celle de transitions de phase. Développée au 19ème siècle pour l’étude des changements d’état de la matière, comme le passage de l’état gazeux à l’état liquide ou de l’état liquide à l’état solide, cette notion a depuis été étendue à bien d’autres états de la matière. C’est ainsi que les cosmologistes ont été amenés à l’idée que les condensations successives qui ont eu lieu après le Big Bang pouvaient être considérées comme des transitions de phase.

Les physiciens distinguent deux types de transitions de phase, les transitions continues et les transitions abruptes. Pour un panorama de l’évolution montrant l’alternance entre des transitions continues et des transitions abruptes, voir mon propre livre [3]. On doit au physicien danois Per Bak d’avoir montré que ces condensations étaient le propre d’un processus d’auto-organisation universel qu’il a baptisé «criticalité auto-organisée» [1]. Pour le lecteur ayant une formation en mathématiques, je recommande le livre de Ricard Solé [4] sur les transitions de phase. Les applications vont de la physique à la biologie et aux sciences humaines. Le dernier chapitre traite plus particulièrement de l’effondrement des sociétés humaines.

Ces processus s’appliquent aux systèmes dits «complexes», c’est-à-dire à des systèmes formés d’un très grand nombre d’éléments (typiquement plusieurs milliards), de même nature (les étoiles d’une galaxie, les molécules d’un gaz, les neurones d’un cerveau ou les individus d’une société) et liés entre eux par des relations non linéaires (voir par exemple [2]). Lorsque ces systèmes évoluent suffisamment lentement, on dit qu’ils sont dans un état quasi-stationnaire. Leur état peut alors être décrit statistiquement par des variables d’ensemble appelées variables macroscopiques ou variables d’état. Dans le cas d’un fluide, ces variables sont, par exemple, la température ou la pression. La relation qui lie entre elles les variables d’état s’appelle l’équation d’état.

Ainsi l’état macroscopique d’une mole [5] de gaz idéal, dit gaz parfait, est entièrement défini par son volume V, sa pression P et sa température absolue T. Ces trois variables sont liées entre elles par l’équation d’état des gaz parfaits PV = RT, où R est une constante appelée constante des gaz parfaits. L’équation d’état des gaz parfaits s’applique aux gaz très peu denses, dont les molécules sont suffisamment éloignées les unes des autres pour qu’on puisse considérer qu’elles n’interagissent pas entre entre elles, sauf au moment des collisions auquel cas leur distance devient négligeable par rapport à leur distance moyenne. C’est le cas de tous les gaz lorsque leur pression est suffisamment faible.

J’ai montré dans ce blog comment ces concepts peuvent être étendus aux sciences humaines. On sait aujourd’hui que la température d’un gaz mesure la vitesse quadratique moyenne d’agitation de ses molécules. Saupoudrez de sucre une fourmilière, vous verrez aussitôt les fourmis s’agiter. On pourrait définir de même la « température » d’une fourmilière comme étant la vitesse quadratique moyenne d’agitation des fourmis. Il est clair que plus le coût de l’énergie est faible, plus l’activité économique est intense et plus les hommes s’agitent comme le font les fourmis dans une fourmilière. Dans mon billet 49, j’ai proposé de définir la température d’une économie comme étant l’inverse du prix de l’énergie.

On peut de même définir une pression économique comme étant une pression sociale au sens de Durkheim. C’est la pression qui incite les individus à acheter tel ou tel produit. Ainsi, pour certaines activités, la possession d’un téléphone portable apporte aujourd’hui un tel avantage qu’il est impossible à la personne concernée de ne pas en acheter un. Dans ce cas, c’est la valeur d’usage qui prime.

Nous avons vu que l’équation du gaz parfait s’applique d’autant mieux que la pression du gaz est plus faible. En économie, on va donc s’attendre à ce qu’elle s’applique au cas ou la pression d’achat est faible. C’est le cas d’une économie d’abondance ou les besoins de chacun sont largement satisfaits. La valeur d’usage de l’objet n’a alors que peu d’intérêt. Ce qui compte, c’est sa valeur d’échange, et celle-ci est d’autant plus grande que l’objet est plus rare ou que son volume V de production est plus faible. C’est le cas des métaux précieux comme l’or ou l’argent, mais aussi des produits de luxe comme les bijoux, les œuvres d’art ou les objets de collection. La pression P d’achat est d’autant plus grande que le volume V de la production est plus faible. On retrouve bien la loi Boyle-Mariotte des gaz parfaits. Elle représente une économie d’individus aisés, libres de toute contrainte liant les uns aux autres, et dont les relations se limitent à des échanges de valeurs au cours d’occasionnelles rencontres: un idéal qu’on nomme le libéralisme.

Dans mon billet 89, j’ai parlé de l’équation proposée en 1873 par van der Waals pour représenter les propriétés des gaz réels. J’ai montré qu’on peut l’appliquer qualitativement à l’économie pour laquelle elle rend compte de la valeur d’usage. L’un des termes correctifs s’applique aux produits de première nécessité: ceux qui correspondent à des dépenses incompressibles. L’autre correspond aux produits dont la valeur d’usage croit avec le nombre d’utilisateurs. C’est le cas des services communs comme les communications ou les transports.

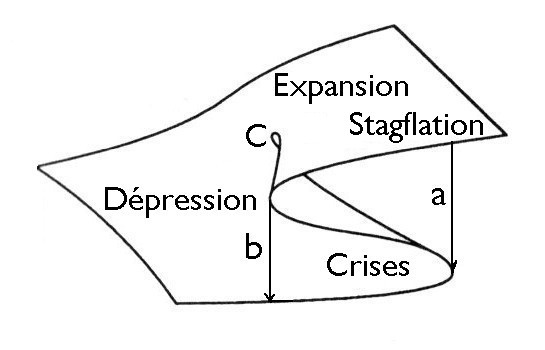
La figure ci-dessus montre l’allure de la surface de van der Waals, appliquée ici à l’économie. On voit qu’elle forme un pli appelé « fronce ». L’origine du pli est le point critique C. Tout point à l’intérieur du pli représente un état du système qui est nécessairement instable. Pour un fluide, il représente un état pour lequelle son volume diminue lorsqu’il se détend, c’est-à-dire un phénomène de condensation. L’état du fluide passe brutalement de la partie supérieure du pli où, vapeur, il occupe un grand volume à sa partie inférieure où, devenu liquide, il occupe un volume beaucoup plus petit. En économie, cela correspond à un effondrement de la production industrielle, souvent lié à une pénurie des moyens de transports.

Les thermodynamiciens appellent ce phénomène de condensation ou d’effondrement une transition de phase abrupte. Une telle transition peut se produire n’importe où entre les flèches marquées a et b sur la figure et n’affecter qu’une partie du système. La transition complète se fait alors plusieurs étapes. Dans le cas d’une économie, on qualifie cette zone d’époque de crises. Statistiquement, la transition se produit à mi-chemin entre les flèches. C’est là que, dans notre billet 90, nous avons plaçé la falaise de Sénèque, mais ce n’est qu’une idéalisation. Tant que la transition n’est pas complète, on dit que le système est dans un état métastable.

Une propriété caractéristique des transitions abruptes est de nécessiter des germes venus du milieu extérieur. Il est courant que ciel soit bleu et l’air limpide alors qu’il est saturé de vapeur d’eau. Il suffit qu’un avion passe pour qu’il laisse une trainée blanche due à la condensation de l’eau. C’est parce que les réacteurs de l’avion ont fourni les germes nécessaires à la condensation sous forme de particules ionisées. De même, l’effondrement d’une société est liée à une influence du milieu extérieur. C’est lui qui déclenche la transition.

On a vu que les structures dissipatives s’auto-organisent en décrivant des cycles autour d’un point critique. Ainsi, en l’absence de perturbations extérieures, une société traverse normalement une phase de dépression, puis une phase d’expansion et une phase de stagflation (voir billet 93). Il s’agit de transitions de phase continues. La société devient alors très sensible à son environnement et traverse une période de crises. Il s’agit d’une transition de phase abrupte. J’en donnerai prochainement de nouveaux exemples historiques.

(1) Per Bak, Quand la nature s’organise: avalanches et tremblements de terre. Flammarion (1999).
(2) Steven H. Strogatz, Nonlinear Dynamics and Chaos, Westview (1994).
(3) François Roddier, Thermodynamique de l’évolution (section 4.4), Parole (2012)
(4) Ricard Solé, Phase Transitions, Princeton (2011).
(5) Une mole ou molécule-gramme contient environ 6 x 1023 atomes.