Dans cet article nous ferons un pas de plus vers l’abstraction. Que le lecteur peu porté vers les notions abstraites me pardonne. Ce sera mon dernier pas dans ce sens. Je reviendrai ensuite peu à peu à des notions plus concrètes, en décrivant ce qui me paraît être les conséquences matérielles de tout ceci.
J’ai comparé (article 19) les flux d’énergie au flux d’une rivière. C’est plus qu’une simple métaphore. L’énergie s’écoule effectivement comme un fluide, mais dans un espace abstrait ayant un très grand nombre de dimensions appelé l’espace des phases. Tel que nous le percevons, l’espace dans lequel nous vivons a trois dimensions. Cela veut dire que pour préciser la position d’un point dans cet espace il faut donner trois nombres ou coordonnées, par exemple sa latitude, sa longitude et son altitude. Pour préciser l’état d’un système mécanique, il faut en général beaucoup plus que trois nombres. La mécanique newtonienne nous apprend que l’évolution d’une masse ponctuelle est entièrement déterminée par sa position et sa vitesse. Aux trois nombres donnant sa position, il faut donc ajouter trois autres nombres donnant sa vitesse en grandeur et en direction. Ainsi pour préciser l’état d’un système mécanique limité à une seule masse ponctuelle il faut 6 nombres, ce qui veut dire que cet état peut être représenté par un point dans un espace à 6 dimensions. C’est l’espace des phases qui décrit l’évolution d’une masse ponctuelle.
Si l’on considère les atomes d’un gaz comme des masses ponctuelles, et si ce gaz contient N atomes, son état sera représenté par un point dans un espace des phases à 6N dimensions. Il est bien entendu impossible de connaître les 6N coordonnées de ce point. On peut tout au plus mesurer une distribution grossière des vitesses et des températures à l’intérieur du gaz. C’est ce qu’on appelle son état macroscopique. De façon générale, à un état macroscopique donné correspond toujours un grand nombre d’états dits microscopiques dont chacun est représenté par un point de l’espace des phases.
L’ensemble de ces points évolue au cours du temps suivant les lois de la mécanique, en particulier la loi de conservation de l’énergie. Cette loi implique que les trajectoires de ces points sont comparables à celles des gouttes d’eau dans une rivière. Un théorème dû au mathématicien français Joseph Liouville nous dit en effet que ces points se déplacent comme les particules d’un fluide incompressible. Tandis qu’une rivière suit la ligne de plus grande pente, notre fluide incompressible n’a pas de direction privilégiée vers laquelle se diriger. Que va-t-il faire? Comme une rivière dans une plaine, il va s’étaler. La rivière y fait des méandres. Notre fluide en fait de même.
Reprenons l’exemple de notre gaz représenté par un point dans un espace à 6N dimensions. L’ensemble des points représentatifs de ce gaz correspondant à une même énergie U se trouvent sur une “hypersurface” de dimension 6N -1. A cause des interactions entre les atomes du gaz, cette hypersurface évolue au cours du temps. On peut montrer qu’elle évolue comme la pâte d’un boulanger qui pétrit son pain, c’est-à-dire par repliement et étirage successifs. Deux points de la pâte initialement proches se retrouvent ainsi rapidement éloignés. C’est pourquoi des conditions initiales suffisamment voisines pour être indiscernables à l’observation, conduisent rapidement à des évolutions très différentes, d’où par exemple la difficulté des prévisions météorologiques.
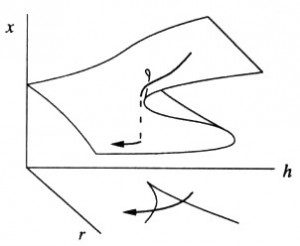
|
| Bifurcation |
Tirée du livre de Steven Strogatz (1), la figure ci-dessus montre une telle surface dans un espace limité à trois dimensions. Le paramètre x est inobservable. Les paramètres r et h sont les paramètres observés. On peut les modifier, c’est-à-dire se déplacer dans le plan horizontal r, h . Prenons comme exemple le déplacement indiqué par la flèche. Au cours de ce déplacement les paramètres r, h varient de façon continue, tandis que le paramètre x peut varier de façon discontinue (saut en pointillé), indiquant un changement brutal et irréversible de notre système. C’est ce que nous avons appelé une bifurcation.
La figure ci-dessus correspond à un type particulier de bifurcation représenté par la courbe en V tracée dans le plan r, h. On doit au mathématicien français René Thom une classification des bifurcations sous le nom de théorie des catastrophes, les restructurations brutales de notre système y étant assimilées à des catastrophes. En évoluant avec le temps, la surface représentée sur la figure va continuer à se replier sur elle-même formant une stucture fractale ((article 18)). Les plis successifs de cette surface engendrent les cascades de bifurcations que nous venons d’étudier.
Ainsi le monde observé ressemble étrangement aux ombres projetées par le feu sur la paroi de la caverne de Platon. Pour comprendre le monde, il faut être capable de reconstituer ce qui se passe dans cet immense espace des phases que nous venons de décrire. La mécanique statistique nous aide à le faire grâce aux lois des grands nombres.
(1) Steven H. Strogatz, Non-linear dynamics and chaos, Westview Press, Perseus, 1994.
Liens internet:
http://fr.wikipedia.org/wiki/Espace_des_phases
http://fr.wikipedia.org/wiki/Joseph_Liouville
http://en.wikipedia.org/wiki/Steven_Strogatz
http://fr.wikipedia.org/wiki/René_Thom
http://pst.chez-alice.fr/TCIvarEk.htm
http://virtualistes.org/platon.htm
Historiquement la mécanique de Newton, l’électromagnétisme de Maxwell, la thermodynamique de Carnot-Clausius, la mécanique quantique, se sont développées plus ou moins indépendamment les unes des autres. L’incompatibilité des théories de Newton et de Maxwell a été résolue par Einstein au détriment de Newton. Dans les autres cas, y a-t-il des théorèmes qui montrent la compatibilité ou des expériences cruciales qui montrent l’incompatibilité?
La preuve que je connais du théorème de Liouville que vous citez nécessite l’existence d’un lagrangien, donc (selon moi) une certaine sorte de conservativité que je sens (je ne suis pas physicien) incompatible avec la dissipativité irréversible qui est, toujours selon moi, l’essence du deuxième principe de la thermodynamique. Autrement dit, à mon avis, le théorème de Liouville ne s’applique pas à la thermodynamique; au doigt mouillé je dirais que le volume d’une portion de l’espace des phases que l’on suit dans son mouvement ne peut qu’augmenter (cf. un théorème de Gromov*): il se comporte comme un fluide incompressible, qui ne peut se comprimer… mais qui peut éventuellement se dilater.
Vous écrivez: « Pour comprendre le monde, il faut être capable de reconstituer ce qui se passe dans cet immense espace des phases que nous venons de décrire. » Je suis d’accord avec cette avant dernière phrase de votre conclusion en ce sens que, selon moi (pas que), la tâche à venir du physicien est dorénavant herméneutique, elle n’est plus démiurgique comme c’est le cas depuis la révolution galiléenne. Une véritable révolution dont l’objectif est de refermer la parenthèse galiléenne.
Quant à la dernière phrase de votre conclusion: « La mécanique statistique nous aide à le faire grâce aux lois des grands nombres », voici ce qu’écrit Thom à ce propos: « Au départ la théorie de la stabilité structurelle m’avait paru d’une telle ampleur et d’une telle généralité qu’avec elle je pouvais espérer en quelque sorte remplacer la thermodynamique par la géométrie, géométriser en un certain sens la thermodynamique, éliminer des considérations thermodynamiques tous les aspects à caractère mesurables et stochastiques pour ne conserver que la caractérisation géométrique correspondante des attracteurs; Il est certain que les phénomènes d’instabilité des attracteurs qu’on a découverts depuis montrent qu’un tel espoir est faux ou, en tout cas, qu’il faudrait profondément modifier la notion de stabilité structurelle en l’affaiblissant de manière considérable. On a beaucoup travaillé à ce genre d’affaiblissement, mais sans avoir trouvé, jusqu’à présent, la bonne conceptualisation. »
Quelques remarques de vocabulaire:
1. La théorie des catastrophes élémentaires n’a pas pour objet une classification des bifurcations mais a à voir avec une classification des dynamiques de gradient les plus simples.
2. La fronce de « bifurcation 2 » n’est ni une bifurcation ni une catastrophe au sens de la théorie thomienne des catastrophes; C’est une singularité au sens de la théorie des singularités des applications (en particulier des projections) de R^p sur R^n, théorie initiée par Whitney dans les années 1950 et développée (entre autres) par Arnold, Thom et Mather.
* https://fr.wikipedia.org/wiki/G%C3%A9om%C3%A9trie_symplectique
Hasard et déterminisme.
En forçant le trait voici comment je résume (ceci n’engage que moi!) les approches choisies par Thom et par Roddier pour tenter de résoudre le problème herméneutique posé par Platon.
Roddier: hasard sûrement, déterminisme peut-être. Thom: déterminisme sûrement, hasard peut-être.
Pour Thom la solution au problème posé par Platon à chercher du côté de la géométrie: il s’agit de reconstituer les êtres dont on ne perçoit que les ombres. Thom part de l’hypothèse que de tels êtres existent, que l’univers primordial n’est pas un chaos.
Pour Roddier elle est à chercher du côté de la thermodynamique et de la physique statistique. Roddier part (je crois!) de l’hypothèse d’un chaos initial immédiatement post big-bang, chaos qui s’auto-organise progressivement.
La « tabula rasa » aristotélicienne vs l’ « être toujours-déjà-là » platonicien? Thom du côté de Platon (« Dieu, toujours, fait de la géométrie »), d’Einstein (« Dieu ne joue pas aux dés »)? Roddier du côté d’Aristote et de Bohr (« Qui es-tu, Albert, pour oser dire à Dieu ce qu’il doit faire?)?
Il est certain que lorsqu’on sait (ou fait l’hypothèse) qu’un tableau carré de nombres qui ont l’air distribués au hasard est la matrice d’une application linéaire, être toujours-déjà-là, on tient une information (une hypothèse de travail) qui influe considérablement sur l’interprétation du tableau. Dans ce cas, l’art de l’herméneute consiste à se placer au bon point de vue, à savoir dans une base de vecteurs propres, où apparaît alors, comme le dit Socrate, « le soleil, non ses vaines images réfléchies dans les eaux ou en quelque autre endroit, mais le soleil lui-même à sa vraie place, qu’il pourra voir et contempler tel qu’il est ».
Le rôle de la chaleur
Quand on mélange deux gaz initialement à des températures distinctes la chaleur diffuse jusqu’à ce que soit atteint l’équilibre thermodynamique. Le désordre du système croît jusqu’à atteindre une valeur maximum (principe du maximum entropique). Et l’évolution vers cet état est considéré comme pratiquement irréversible. La chaleur met donc de l’ordre macroscopique à l’intérieur de l’enceinte (puisqu’elle tend à y uniformiser la température) en y mettant le désordre microscopique maximum.
Dans l’hypothèse d’une vision métaphysique du type « éternel retour », on peut imaginer un « être-toujours-déjà-là » caractérisé par sa topologie toujours-déjà-la-même, qui peut prendre diverses apparences géométriques, des plus chaotiques (juste après le big bang) aux plus ordonnées (juste avant?).
L’hypothèse faite sur l’invariance topologique de l’être fait que, lors du big bang, les morceaux de l’être-toujours-déjà-là se dispersent aux quatre vents, en gardant néanmoins en mémoire leur position relative par rapport à leurs voisins* (autrement dit en gardant la mémoire de la topologie).
On est alors dans une situation semblable à celle d’une application linéaire, être-toujours-déjà-là, dont on prend la matrice dans une base prise au hasard (juste après le big bang) ou dans une base de vecteurs propres (juste avant?).
Il s’agit de trouver une représentation propre, intelligible, à partir d’une représentation chaotique. Une méthode naturelle(?) consiste à laisser agir la douce chaleur. Supposons par exemple que l’être soit un cercle topologique à n points p0, p1,…, pn, avec pn=p0, n=100 pour fixer les idées. On part d’une situation chaotique où les 100 points sont répartis aléatoirement sur l’écran de l’ordinateur et on fait évoluer le cercle en remplaçant (par exemple) pi par (pi-1 + 2pi + pi+1)/4, i=0,…,100. En réitérant cette procédure, on voit les points de l’écran se concentrer de plus en plus au barycentre (centre de « gravité ») des n points. Mais si on prend la précaution** de renormaliser à chaque étape (ou seulement de temps à autre) de façon à occuper tout l’écran, on voit peu à peu les points s’organiser pour se mettre géométriquement (et non seulement topologiquement) en cercle (ou plutôt en ellipse pour la renormalisation la plus simple). La programmation est triviale et l’évolution est assez fascinante à suivre avec des surfaces (bande de Moëbius, tore, bouteille de Klein, cross-cap, surface de Boy, etc.).
*: Deux électrons, par exemple, à ce jour l’un sur notre terre, l’autre sur Sirius, ayant gardé mémoire de leur proximité initiale.
**: Peut-être la Nature ne prend-elle pas cette précaution et c’est pour ça que ça finit par exploser!